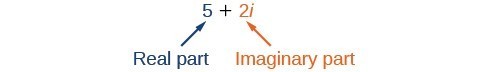- Understand the difference between imaginary numbers and complex numbers
- Learn how to plot a complex number on a special graph called the complex plane
- Perform calculations with complex numbers and visualize how these operations change their position and size when graphed
- Find the points where a quadratic equation crosses the x-axis, including both real and complex solutions
Complex Numbers
We know how to find the square root of any positive real number. In a similar way we can find the square root of a negative number. The difference is that the root is not real. If the value in the radicand is negative, the root is said to be an imaginary number. The imaginary number [latex]i[/latex] is defined as the square root of negative 1.
[latex]\sqrt{-1}=i[/latex]
So, using properties of radicals,
[latex]{i}^{2}={\left(\sqrt{-1}\right)}^{2}=-1[/latex]
We can write the square root of any negative number as a multiple of [latex]i[/latex].
[latex]\begin{align}\sqrt{-25}&=\sqrt{25\cdot \left(-1\right)}\\&=\sqrt{25}\cdot\sqrt{-1}\\ &=5i\end{align}[/latex]
We use [latex]5i[/latex] and not [latex]-\text{5}i[/latex] because the principal root of [latex]25[/latex] is the positive root.
imaginary number
The imaginary number [latex]i[/latex] is defined to be [latex]i=\sqrt{-1}[/latex].
Any real multiple of [latex]i[/latex], like 5[latex]i[/latex], is also an imaginary number.
Example: [latex]\sqrt{9}=3[/latex] because [latex]3 \ast 3 = 9[/latex].
It is also true that [latex](-3)\ast (-3) = 9[/latex] although we agreed that using the radical symbol requests only the principle root, the positive one. But, there is no number that when multiplied by itself results in a negative number.
The property of integer multiplication states that both a negative number squared and a positive number squared result in a positive number. Indeed, you saw in the review section to this module that the square root of a negative number does not exist in the set of real numbers. Mathematicians realized the helpfulness of being to do calculations with such numbers though, so they assigned a value to [latex]\sqrt{-1}[/latex], calling it the imaginary unit [latex]i[/latex].
A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written [latex]a+bi[/latex] where [latex]a[/latex] is the real part and [latex]bi[/latex] is the imaginary part.
complex number
A complex number is a number [latex]z = a + b i[/latex], where
- [latex]a[/latex] and [latex]b[/latex] are real numbers
- [latex]a[/latex] is the real part of the complex number
- [latex]b[/latex] is the imaginary part of the complex number