Intersection of a Circle and a Line
Now that we’ve got a solid understanding of circles and how to write their equations, let’s explore what happens when a circle intersects with a line. This is a common situation in algebra and geometry, and it’s fascinating to see how these two shapes interact. By analyzing the intersection points, we can solve various real-world problems, from finding the shortest path to designing curves in engineering.
When we talk about the intersection of a circle and a line, we’re essentially looking for points that satisfy both the equation of the circle and the equation of the line simultaneously. This creates a system of equations:
- The circle equation: [latex](x - h)^2 + (y - k)^2 = r^2[/latex]
- The line equation: [latex]y = mx + b[/latex]
Solving this system will give us the points where the line meets the circle, if any.
- Substitute the equation of the line into the equation of the circle
- Simplify and rearrange to get a quadratic equation in terms of [latex]x[/latex] (or [latex]y[/latex])
- Solve the quadratic equation
- Use the solutions to find the corresponding [latex]y[/latex]-values (or [latex]x[/latex]-values)
The nature of the solutions to the quadratic equation tells us about the intersection:
- No real solutions: The line doesn’t intersect the circle
- One real solution: The line is tangent to the circle
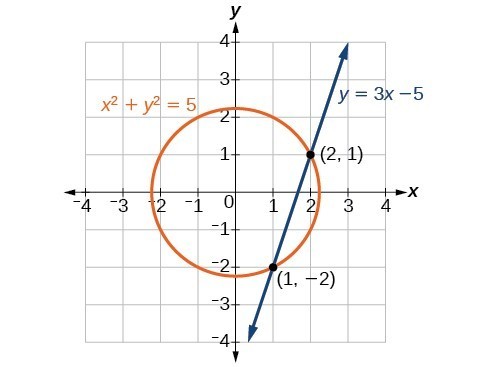
- Two real solutions: The line crosses through the circle
types of solutions for the points of intersection of a circle and a line
There are [latex]3[/latex] possible solution sets for a system of equations involving a circle and a line.

- No solution.
- The line does not intersect the circle.
- One solution.
- The line is tangent to the circle and intersects the circle at exactly one point.
- Two solutions.
- The line crosses the circle and intersects it at two points.