General Form of the Equation of a Circle
In algebra, circles can be described using different equations. One common way is the general form, which can look a bit complicated at first. This form doesn’t directly show the center or the radius of the circle, making it harder to visualize and can be a little tricky to work with.
general form of the equation of a circle
The general form of the equation of a circle is:
[latex]x^2+y^2+ax+by+c = 0[/latex]
To make things clearer, we often convert the general form to another version known as the standard form, [latex](x-h)^2+(y-k)^2 = r^2[/latex]. This transformation involves a process called completing the square, in both [latex]x[/latex] and [latex]y[/latex], which helps us easily identify the circle’s center and radius. Then, we can graph the circle using its center and radius.
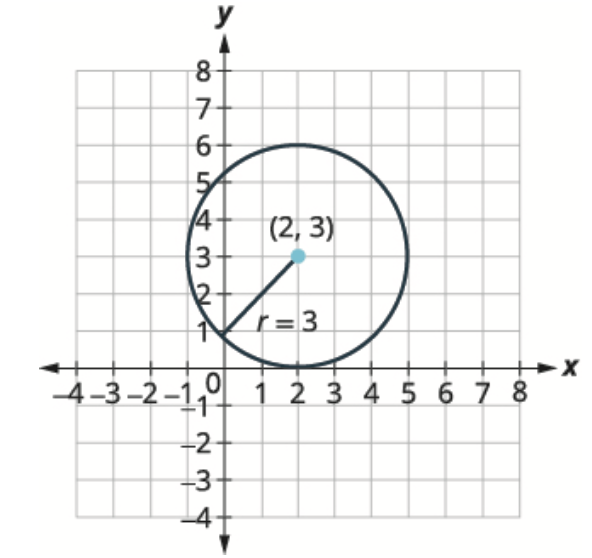
Find the center and radius, then graph the circle:
[latex]x^2+y^2-4x-6y+4 = 0[/latex]