- Write the equations for circles using the standard form
- Graph a circle
- Solve system of equations involving circles
Write the Equation of a Circle in Standard Form
The Main Idea
- Circle Definition:
- Set of points equidistant from a center point in a plane
- Center: [latex](h,k)[/latex]
- Radius: [latex]r[/latex]
- Standard Form Equation:
- [latex](x-h)^2+(y-k)^2 = r^2[/latex]
- [latex](h,k)[/latex] represents the center
- [latex]r[/latex] is the radius
- Components of the Equation:
- [latex](x-h)^2[/latex]: horizontal distance from center
- [latex](y-k)^2[/latex]: vertical distance from center
- Right side [latex]r^2[/latex]: squared radius
- Variations:
- Center at origin: [latex]x^2+y^2 = r^2[/latex]
- Negative values inside parentheses change to addition
You can view the transcript for “Ex 1: Write General Equation of a Circle in Standard Form” here (opens in new window).
Graph a Circle
The Main Idea
- Equation to Graph Relationship:
- Standard form: [latex](x-h)^2 + (y-k)^2 = r^2[/latex]
- Each part of the equation corresponds to a graphical feature
- Key Components for Graphing:
- Center: [latex](h,k)[/latex]
- Radius: [latex]r[/latex] (square root of the right side)
- Critical Points:
- Center: [latex](h,k)[/latex]
- Top: [latex](h, k+r)[/latex]
- Bottom: [latex](h, k-r)[/latex]
- Right: [latex](h+r, k)[/latex]
- Left: [latex](h-r, k)[/latex]
- Symmetry:
- Circles are symmetrical about their center
- Vertical and horizontal lines through the center are lines of symmetry
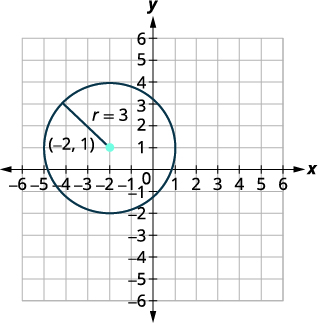
Graph the circle given by the equation: [latex](x+1)^2 + (y-3)^2 = 9[/latex]
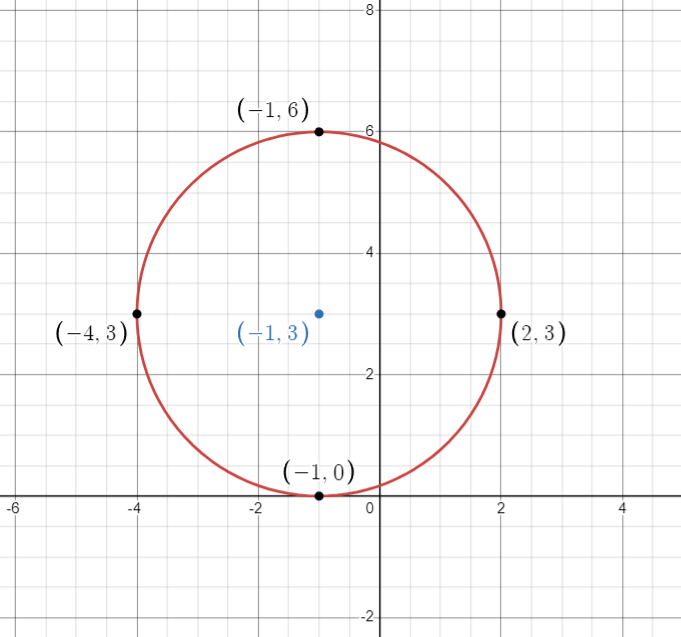
You can view the transcript for “Graph a Circle: Write the Equation in Standard form x^2+y^2-10y+16=0” here (opens in new window).
General Form of the Equation of a Circle
The Main Idea
- General Form Equation:
- [latex]x^2 + y^2 + ax + by + c = 0[/latex]
- [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are constants
- Does not directly show center or radius
- Comparison with Standard Form:
- Standard Form: [latex](x-h)^2+(y-k)^2 = r^2[/latex]
- Center: [latex](h, k)[/latex]
- Radius: [latex]r[/latex]
- Conversion Process:
- Use completing the square for both x and y terms
- Transforms general form to standard form
- Reveals center and radius
- Importance of Conversion:
- Makes graphing easier
- Helps in identifying key circle properties
Finding the Equation of a Circle
The Main Idea
- Standard Form Equation: [latex](x - h)^2 + (y - k)^2 = r^2[/latex]
- [latex](h, k)[/latex] is the center
- [latex]r[/latex] is the radius
- Three Common Scenarios:
- Known center and radius
- Known center and a point on the circle
- Known two points on the circle (often diameter endpoints)
- Key Formulas:
- Distance Formula: [latex]d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}[/latex]
- Midpoint Formula: [latex]\left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)[/latex]
Scenario Breakdown
Scenario 1: Known Center and Radius
- Directly plug into standard form equation
Scenario 2: Known Center and Point
- Use distance formula to find radius
- Plug center and calculated radius into standard form
Scenario 3: Two Points on Circle
- Use midpoint formula to find center
- Use distance formula to find radius (center to either point)
- Plug center and calculated radius into standard form
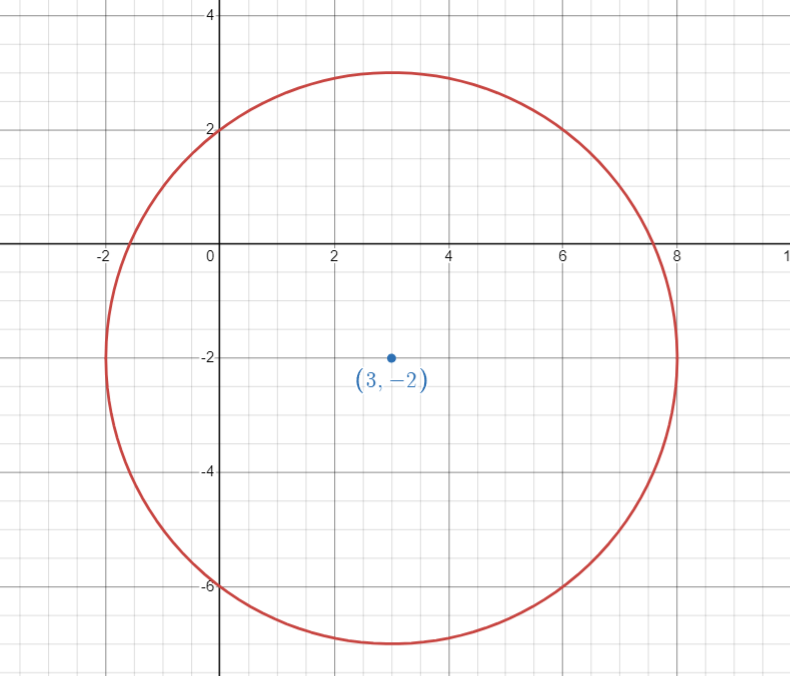
You can view the transcript for “Ex: Find Standard Equation of a Circle Given Center and Point on the Circle” here (opens in new window).
Intersection of a Circle and a Line
The Main Idea
- System of Equations:
- Circle: [latex](x - h)^2 + (y - k)^2 = r^2[/latex]
- Line: [latex]y = mx + b[/latex]
- Solving Process:
- Substitute line equation into circle equation
- Solve resulting quadratic equation
- Types of Intersections:
- No intersection: No real solutions
- Tangent: One real solution
- Two intersections: Two real solutions
- Geometric Interpretation:
- No intersection: Line outside circle
- One intersection: Line touches circle at one point
- Two intersections: Line passes through circle
Solution Process
- Substitute [latex]y = mx + b[/latex] into circle equation
- Simplify to get quadratic in [latex]x[/latex]: [latex]ax^2 + bx + c = 0[/latex]
- Solve quadratic using preferred method (factoring, quadratic formula, etc.)
- Find corresponding [latex]y[/latex]-values using line equation
- Check solutions in both original equations
You can view the transcript for “Ex 2: Find a Point of Intersection of a Line and a Circle” here (opens in new window).