Combinations and Compositions of Functions
For the following exercises, determine the domain for each function in interval notation.
- Given [latex]f(x) = x^2 + 2x[/latex] and [latex]g(x) = 6 - x^2[/latex], find [latex]f + g[/latex], [latex]f - g[/latex], [latex]fg[/latex], and [latex]\dfrac{f}{g}[/latex].
- Given [latex]f(x) = 2x^2 + 4x[/latex] and [latex]g(x) = \dfrac{1}{2x}[/latex], find [latex]f + g[/latex], [latex]f - g[/latex], [latex]fg[/latex], and [latex]\dfrac{f}{g}[/latex].
- Given [latex]f(x) = 3x^2[/latex] and [latex]g(x) = \sqrt{x - 5}[/latex], find [latex]f + g[/latex], [latex]f - g[/latex], [latex]fg[/latex], and [latex]\dfrac{f}{g}[/latex].
For the following exercise, find the indicated function given [latex]f(x) = 2x^2 + 1[/latex] and [latex]g(x) = 3x - 5[/latex].
-
- [latex]f(g(2))[/latex]
- [latex]f(g(x))[/latex]
- [latex]g(f(x))[/latex]
- [latex](g \circ g)(x)[/latex]
- [latex](f \circ f)(-2)[/latex]
For the following exercises, use each pair of functions to find [latex]f(g(x))[/latex] and [latex]g(f(x))[/latex]. Simplify your answers.
- Given [latex]f(x) = \sqrt{x} + 2[/latex] and [latex]g(x) = x^2 + 3[/latex], find [latex]f(g(x))[/latex] and [latex]g(f(x))[/latex].
- Given [latex]f(x) = \sqrt[3]{x}[/latex] and [latex]g(x) = \dfrac{x + 1}{x^3}[/latex], find [latex]f(g(x))[/latex] and [latex]g(f(x))[/latex].
- Given [latex]f(x) = \dfrac{1}{x - 4}[/latex] and [latex]g(x) = \dfrac{2}{x} + 4[/latex], find [latex]f(g(x))[/latex] and [latex]g(f(x))[/latex].
For the following exercises, use each set of functions to find [latex]f(g(h(x)))[/latex]. Simplify your answers.
- Given [latex]f(x) = x^2 + 1[/latex], [latex]g(x) = \dfrac{1}{x}[/latex], and [latex]h(x) = x + 3[/latex], find [latex]f(g(h(x)))[/latex].
- Given [latex]f(x) = \sqrt{2 - 4x}[/latex] and [latex]g(x) = -\dfrac{3}{x}[/latex], find the following:
- [latex](g \circ f)(x)[/latex]
- The domain of [latex](g \circ f)(x)[/latex] in interval notation
- Given the functions [latex]p(x) = \dfrac{1}{\sqrt{x}}[/latex] and [latex]m(x) = x^2 - 4[/latex], state the domain of each of the following functions using interval notation:
- [latex]\dfrac{p(x)}{m(x)}[/latex]
- [latex]p(m(x))[/latex]
- [latex]m(p(x))[/latex]
- For [latex]f(x) = \dfrac{1}{x}[/latex] and [latex]g(x) = \sqrt{x - 1}[/latex], write the domain of [latex](f \circ g)(x)[/latex] in interval notation.
For the following exercises, find functions [latex]f(x)[/latex] and [latex]g(x)[/latex] so the given function can be expressed as [latex]h(x) = f(g(x))[/latex].
- [latex]h(x) = (x - 5)^3[/latex]
- [latex]h(x) = \dfrac{4}{(x+2)^2}[/latex]
- [latex]h(x) = \sqrt[3]{\dfrac{1}{2x - 3}}[/latex]
- [latex]h(x) = \sqrt[4]{\dfrac{3x - 2}{x + 5}}[/latex]
- [latex]h(x) = \sqrt{2x + 6}[/latex]
- [latex]h(x) = \sqrt[3]{x - 1}[/latex]
- [latex]h(x) = \dfrac{1}{(x - 2)^3}[/latex]
- [latex]h(x) = \sqrt{\dfrac{2x-1}{3x+4}}[/latex]
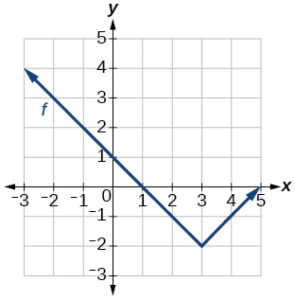
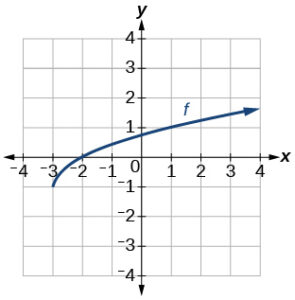
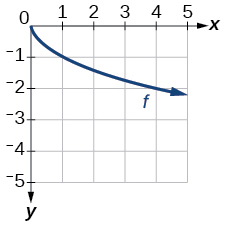
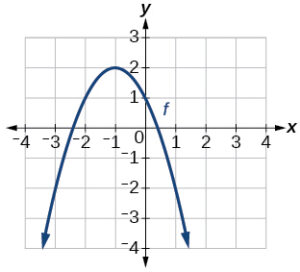
For the following exercises, use the graphs of [latex]f[/latex], shown in the first graph, and [latex]g[/latex], shown in the second graph, to evaluate the expressions.
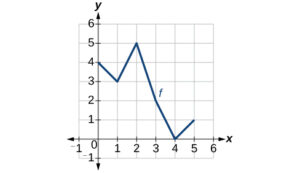
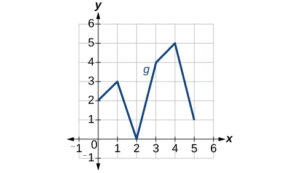
- [latex]f(g(1))[/latex]
- [latex]g(f(0))[/latex]
- [latex]f(f(4))[/latex]
- [latex]g(g(0))[/latex]
For the following exercises, use graphs of [latex]f(x)[/latex], [latex]g(x)[/latex], and [latex]h(x)[/latex], to evaluate the expressions.
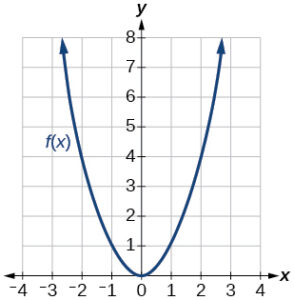
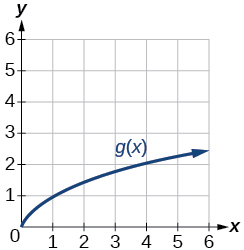
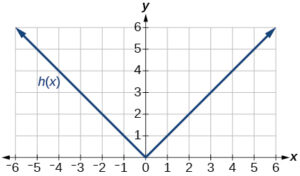
- [latex]g(f(2))[/latex]
- [latex]f(g(1))[/latex]
- [latex]h(f(2))[/latex]
- [latex]f(g(f(-2)))[/latex]
For the following exercises, use the function values for [latex]f[/latex] and [latex]g[/latex] shown in the table below to evaluate each expression.
| [latex]x[/latex] | [latex]f(x)[/latex] | [latex]g(x)[/latex] |
|---|---|---|
| [latex]0[/latex] | [latex]7[/latex] | [latex]9[/latex] |
| [latex]1[/latex] | [latex]6[/latex] | [latex]5[/latex] |
| [latex]2[/latex] | [latex]5[/latex] | [latex]6[/latex] |
| [latex]3[/latex] | [latex]8[/latex] | [latex]2[/latex] |
| [latex]4[/latex] | [latex]4[/latex] | [latex]1[/latex] |
| [latex]5[/latex] | [latex]0[/latex] | [latex]8[/latex] |
| [latex]6[/latex] | [latex]2[/latex] | [latex]7[/latex] |
| [latex]7[/latex] | [latex]1[/latex] | [latex]3[/latex] |
| [latex]8[/latex] | [latex]9[/latex] | [latex]4[/latex] |
| [latex]9[/latex] | [latex]3[/latex] | [latex]0[/latex] |
- [latex]f(g(5))[/latex]
- [latex]g(f(3))[/latex]
- [latex]f(f(1))[/latex]
- [latex]g(g(6))[/latex]
For the following exercises, use the function values for [latex]f[/latex] and [latex]g[/latex] shown in the table below to evaluate the expressions.
| [latex]x[/latex] | [latex]f(x)[/latex] | [latex]g(x)[/latex] |
|---|---|---|
| [latex]-3[/latex] | [latex]11[/latex] | [latex]-8[/latex] |
| [latex]-2[/latex] | [latex]9[/latex] | [latex]-3[/latex] |
| [latex]-1[/latex] | [latex]7[/latex] | [latex]0[/latex] |
| [latex]0[/latex] | [latex]5[/latex] | [latex]1[/latex] |
| [latex]1[/latex] | [latex]3[/latex] | [latex]0[/latex] |
| [latex]2[/latex] | [latex]1[/latex] | [latex]-3[/latex] |
| [latex]3[/latex] | [latex]-1[/latex] | [latex]-8[/latex] |
- [latex](f \circ g)(1)[/latex]
- [latex](g \circ f)(3)[/latex]
- [latex](f \circ f)(3)[/latex]
For the following exercises, use each pair of functions to find [latex]f(g(0))[/latex] and [latex]g(f(0))[/latex].
- [latex]f(x) = 5x + 7[/latex], [latex]g(x) = 4 - 2x^2[/latex]
- [latex]f(x) = \dfrac{1}{x+2}[/latex], [latex]g(x) = 4x + 3[/latex]
For the following exercises, use the functions [latex]f(x) = 2x^2 + 1[/latex] and [latex]g(x) = 3x + 5[/latex] to evaluate or find the composite function as indicated.
- [latex]f(g(x))[/latex]
- [latex](g \circ g)(x)[/latex]
Real-World Applications.
- The function [latex]A(d)[/latex] gives the pain level on a scale of [latex]0[/latex] to [latex]10[/latex] experienced by a patient with [latex]d[/latex] milligrams of a pain-reducing drug in her system. The milligrams of the drug in the patient’s system after [latex]t[/latex] minutes is modeled by [latex]m(t)[/latex]. Which of the following would you do in order to determine when the patient will be at a pain level of [latex]4[/latex]?
- Evaluate [latex]A(m(4))[/latex].
- Evaluate [latex]m(A(4))[/latex].
- Solve [latex]A(m(t)) = 4[/latex].
- Solve [latex]m(A(d)) = 4[/latex].
- A rain drop hitting a lake makes a circular ripple. If the radius, in inches, grows as a function of time in minutes according to [latex]r(t) = 25\sqrt{t} + 2[/latex], find the area of the ripple as a function of time. Find the area of the ripple at [latex]t = 2[/latex].
- Use the function you found in the previous exercise to find the total area burned after [latex]5[/latex] minutes.
- The number of bacteria in a refrigerated food product is given by [latex]N(T) = 23T^2 - 56T + 1[/latex], [latex]3 < T < 33[/latex], where [latex]T[/latex] is the temperature of the food. When the food is removed from the refrigerator, the temperature is given by [latex]T(t) = 5t + 1.5[/latex], where [latex]t[/latex] is the time in hours.
- Find the composite function [latex]N(T(t))[/latex].
- Find the time (round to two decimal places) when the bacteria count reaches [latex]6752[/latex].
Transformations of Functions
For the following exercises, write a formula for the function obtained when the graph is shifted as described.
- [latex]f(x) = |x|[/latex] is shifted down 3 units and to the right 1 unit.
- [latex]f(x) = \dfrac{1}{x^2}[/latex] is shifted up 2 units and to the left 4 units.
For the following exercises, describe how the graph of the function is a transformation of the graph of the original function [latex]f[/latex].
- [latex]y = f(x + 43)[/latex]
- [latex]y = f(x - 4)[/latex]
- [latex]y = f(x) + 8[/latex]
- [latex]y = f(x) - 7[/latex]
- [latex]y = f(x + 4) - 1[/latex]
For the following exercises, determine the interval(s) on which the function is increasing and decreasing.
- [latex]g(x) = 5(x + 3)^2 - 2[/latex]
- [latex]k(x) = -3\sqrt{x - 1}[/latex]
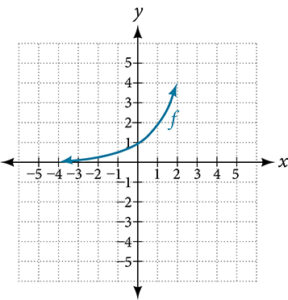
- Use the graph of [latex]f(x) = 2^x[/latex] to sketch a graph of the transformation of [latex]f(x)[/latex], [latex]h(x) = 2^x - 3[/latex].
For the following exercises, sketch a graph of the function as a transformation of the graph of one of the toolkit functions.
- [latex]f(t) = (t + 1)^2 - 3[/latex]
- [latex]k(x) = (x - 2)^3 - 1[/latex]
- Tabular representations for the functions [latex]f[/latex], [latex]g[/latex], and [latex]h[/latex] are given below. Write [latex]g(x)[/latex] and [latex]h(x)[/latex] as transformations of [latex]f(x)[/latex].
[latex]x[/latex] [latex]-2[/latex] [latex]-1[/latex] [latex]0[/latex] [latex]1[/latex] [latex]2[/latex] [latex]f(x)[/latex] [latex]-2[/latex] [latex]-1[/latex] [latex]-3[/latex] [latex]1[/latex] [latex]2[/latex] [latex]x[/latex] [latex]-1[/latex] [latex]0[/latex] [latex]1[/latex] [latex]2[/latex] [latex]3[/latex] [latex]g(x)[/latex] [latex]-2[/latex] [latex]-1[/latex] [latex]-3[/latex] [latex]1[/latex] [latex]2[/latex] [latex]x[/latex] [latex]-2[/latex] [latex]-1[/latex] [latex]0[/latex] [latex]1[/latex] [latex]2[/latex] [latex]h(x)[/latex] [latex]-1[/latex] [latex]0[/latex] [latex]-2[/latex] [latex]2[/latex] [latex]3[/latex]
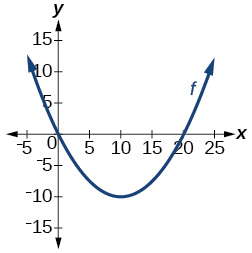
For the following exercises, write an equation for each graphed function by using transformations of the graphs of one of the toolkit functions.
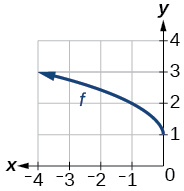
For the following exercises, use the graphs of transformations of the square root function to find a formula for each of the functions.
For the following exercises, use the graphs of the transformed toolkit functions to write a formula for each of the resulting functions.
For the following exercises, determine whether the function is odd, even, or neither.
-
-
- [latex]f(x) = 3x^4[/latex]
- [latex]h(x) = \dfrac{1}{x} + 3x[/latex]
- [latex]g(x) = 2x^4[/latex]
-
For the following exercises, describe how the graph of each function is a transformation of the graph of the original function [latex]f[/latex].
-
-
- [latex]g(x) = -f(x)[/latex]
- [latex]g(x) = 4f(x)[/latex]
- [latex]g(x) = f(5x)[/latex]
- [latex]g(x) = f\left(\dfrac{1}{3}x\right)[/latex]
- [latex]g(x) = 3f(-x)[/latex]
-
For the following exercises, write a formula for the function [latex]g[/latex] that results when the graph of a given toolkit function is transformed as described.
-
-
- The graph of [latex]f(x) = |x|[/latex] is reflected over the [latex]y[/latex]-axis and horizontally compressed by a factor of [latex]\dfrac{1}{4}[/latex].
- The graph of [latex]f(x) = \dfrac{1}{x^2}[/latex] is vertically compressed by a factor of [latex]\dfrac{1}{3}[/latex], then shifted to the left [latex]2[/latex] units and down [latex]3[/latex] units.
- The graph of [latex]f(x) = x^2[/latex] is vertically compressed by a factor of [latex]\dfrac{1}{2}[/latex], then shifted to the right [latex]5[/latex] units and up [latex]1[/latex] unit.
-
For the following exercises, describe how the formula is a transformation of a toolkit function. Then sketch a graph of the transformation.
-
-
- [latex]g(x) = 4(x + 1)^2 - 5[/latex]
- [latex]h(x) = -2 |x - 4| + 3[/latex]
- [latex]m(x) = \dfrac{1}{2} x^3[/latex]
- [latex]p(x) = \left(\dfrac{1}{3} x\right)^3 - 3[/latex]
- [latex]a(x) = \sqrt{-x + 4}[/latex]
-
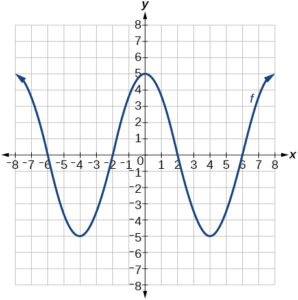
For the following exercises, use the graph below to sketch the given transformations.
-
-
- [latex]g(x) = -f(x)[/latex]
- [latex]g(x) = f(x - 2)[/latex]
-
Inverse Functions
For the following exercises, find [latex]f^{-1}(x)[/latex] for each function.
-
-
- [latex]f(x) = x + 3[/latex]
- [latex]f(x) = 2 - x[/latex]
- [latex]f(x) = \dfrac{x}{x + 2}[/latex]
-
For the following exercises, find a domain on which each function [latex]f[/latex] is one-to-one and non-decreasing. Write the domain in interval notation. Then find the inverse of [latex]f[/latex] restricted to that domain.
-
-
- [latex]f(x) = (x + 7)^2[/latex]
- [latex]f(x) = x^2 - 5[/latex]
-
For the following exercises, use function composition to verify that [latex]f(x)[/latex] and [latex]g(x)[/latex] are inverse functions.
-
-
- [latex]f(x) = \sqrt[3]{x - 1}[/latex] and [latex]g(x) = x^3 + 1[/latex]
-
For the following exercises, use a graphing utility to determine whether each function is one-to-one.
-
-
- [latex]f(x) = \sqrt{x}[/latex]
- [latex]f(x) = -5x + 1[/latex]
-
For the following exercises, determine whether the graph represents a one-to-one function.
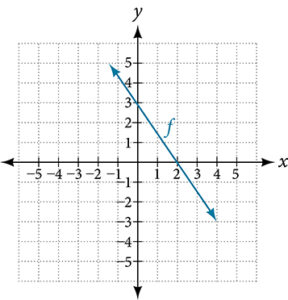
For the following exercises, use the graph of f shown in Figure 11.
-
-
- Find [latex]f(0)[/latex].
- Find [latex]f^{-1}(0)[/latex].
-
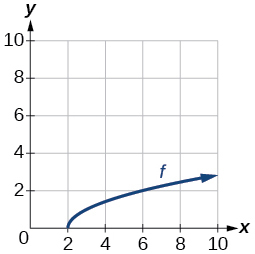
For the following exercises, use the graph of the one-to-one function shown in Figure 12.
-
-
- Sketch the graph of [latex]f^{-1}[/latex].
- If the complete graph of [latex]f[/latex] is shown, find the domain of [latex]f[/latex].
-
For the following exercises, evaluate or solve, assuming that the function [latex]f[/latex] is one-to-one.
-
-
- If [latex]f(6) = 7[/latex], find [latex]f^{-1}(7)[/latex].
- If [latex]f^{-1}(-4) = -8[/latex], find [latex]f(-8)[/latex].
-
For the following exercises, use the values listed in Table 6 to evaluate or solve.
| [latex]x[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] | [latex]7[/latex] | [latex]8[/latex] | [latex]9[/latex] |
|---|---|---|---|---|---|---|---|---|---|---|
| [latex]f(x)[/latex] | [latex]8[/latex] | [latex]0[/latex] | [latex]7[/latex] | [latex]4[/latex] | [latex]2[/latex] | [latex]6[/latex] | [latex]5[/latex] | [latex]3[/latex] | [latex]9[/latex] | [latex]1[/latex] |
-
-
- Find [latex]f(1)[/latex].
- Find [latex]f^{-1}(0)[/latex].
-
Use the tabular representation of [latex]f[/latex] in Table 7 to create a table for [latex]f^{-1}(x)[/latex].
| [latex]x[/latex] | [latex]3[/latex] | [latex]6[/latex] | [latex]9[/latex] | [latex]13[/latex] | [latex]14[/latex] |
|---|---|---|---|---|---|
| [latex]f(x)[/latex] | [latex]1[/latex] | [latex]4[/latex] | [latex]7[/latex] | [latex]12[/latex] | [latex]16[/latex] |
-
- To convert from [latex]x[/latex] degrees Celsius to [latex]y[/latex] degrees Fahrenheit, we use the formula [latex]f(x) = \dfrac{9}{5} x + 32[/latex]. Find the inverse function, if it exists, and explain its meaning.
- A car travels at a constant speed of 50 miles per hour. The distance the car travels in miles is a function of time, [latex]t[/latex], in hours given by [latex]d(t) = 50t[/latex]. Find the inverse function by expressing the time of travel in terms of the distance traveled. Call this function [latex]t(d)[/latex]. Find [latex]t(180)[/latex] and interpret its meaning.