Sequences and Their Notations
For the following exercises, write the first four terms of the sequence.
- [latex]a_n = -\frac{16}{n+1}[/latex]
- [latex]a_n = \frac{2^n}{n^3}[/latex]
- [latex]a_n = 1.25 \cdot (-4)^{n-1}[/latex]
- [latex]a_n = \frac{n^2}{2n+1}[/latex]
- [latex]a_n = -\left(\frac{4 \cdot (-5)^{n-1}}{5}\right)[/latex]
For the following exercises, write the first eight terms of the piecewise sequence.
- [latex]a_n = \begin{cases} \frac{n^2}{2n+1} & \text{if } n \leq 5 \ n^2 - 5 & \text{if } n > 5 \end{cases}[/latex]
- [latex]a_n = \begin{cases} -0.6 \cdot 5^{n-1} & \text{if } n \text{ is prime or } 1 \ 2.5 \cdot (-2)^{n-1} & \text{if } n \text{ is composite} \end{cases}[/latex]
For the following exercises, write an explicit formula for each sequence.
- [latex]4, \ 7, \ 12, \ 19, \ 28, \ \dots[/latex]
- [latex]1, \ 1, \ \frac{4}{3}, \ 2, \ \frac{16}{5}, \ \dots[/latex]
- [latex]1, \ -\frac{1}{2}, \ \frac{1}{4}, \ -\frac{1}{8}, \ \frac{1}{16}, \ \dots[/latex]
For the following exercises, write the first five terms of the sequence.
- [latex]a_1 = 3, \quad a_n = (-3) , a_{n-1}[/latex]
- [latex]a_1 = -1, \quad a_n = \frac{(-3)^{n-1}}{a_{n-1} - 2}[/latex]
For the following exercises, write the first eight terms of the sequence.
- [latex]a_1 = \frac{1}{24}, \quad a_2 = 1, \quad a_n = (2 a_{n-2})(3 a_{n-1})[/latex]
- [latex]a_1 = 2, \quad a_2 = 10, \quad a_n = \frac{2(a_{n-1} + 2)}{a_{n-2}}[/latex]
For the following exercises, write a recursive formula for each sequence.
- [latex]-8, \ -6, \ -3, \ 1, \ 6, \ \dots[/latex]
- [latex]35, \ 38, \ 41, \ 44, \ 47, \ \dots[/latex]
For the following exercises, evaluate the factorial.
- [latex]6![/latex]
- [latex]\frac{12!}{6!}[/latex]
For the following exercises, write the first four terms of the sequence.
- [latex]a_n = \frac{n!}{n^2}[/latex]
- [latex]a_n = \frac{n!}{n^2 - n - 1}[/latex]
For the following exercises, graph the first five terms of the indicated sequence
- [latex]a_n = \frac{(-1)^n}{n} + n[/latex]
- [latex]a_1 = 2, \quad a_n = (-a_{n-1} + 1)^2[/latex]
- [latex]a_n = \frac{(n+1)!}{(n-1)!}[/latex]
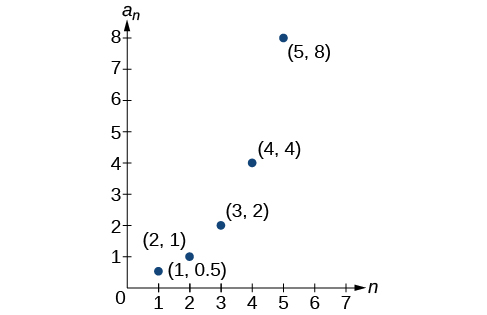
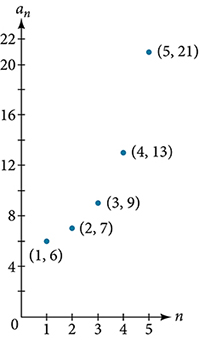
For the following exercise, write an explicit formula for the sequence using the first five points shown on the graph.
For the following exercise, write a recursive formula for the sequence using the first five points shown on the graph.
Arithmetic Sequences
For the following exercise, find the common difference for the arithmetic sequence provided.
- [latex]{0, \ \frac{1}{2}, \ 1, \ \frac{3}{2}, \ 2, \ \dots }[/latex]
For the following exercise, determine whether the sequence is arithmetic. If so find the common difference.
- [latex]{4, \ 16, \ 64, \ 256, \ 1024, \ \dots }[/latex]
For the following exercise, write the first five terms of the arithmetic sequence given the first term and common difference.
- [latex]a_1 = 0, \quad d = \frac{2}{3}[/latex]
For the following exercise, write the first five terms of the arithmetic series given two terms.
- [latex]a_{13} = -60, \quad a_{33} = -160[/latex]
For the following exercises, find the specified term for the arithmetic sequence given the first term and common difference.
- First term is [latex]4[/latex], common difference is [latex]5[/latex], find the [latex]4^{\text{th}}[/latex] term.
- First term is [latex]6[/latex], common difference is [latex]7[/latex], find the [latex]6^{\text{th}}[/latex] term.
For the following exercises, find the first term given two terms from an arithmetic sequence.
- Find the first term or [latex]a_1[/latex] of an arithmetic sequence if [latex]a_6 = 12[/latex] and [latex]a_{14} = 28[/latex].
- Find the first term or [latex]a_1[/latex] of an arithmetic sequence if [latex]a_8 = 40[/latex] and [latex]a_{23} = 115[/latex].
- Find the first term or [latex]a_1[/latex] of an arithmetic sequence if [latex]a_{11} = 11[/latex] and [latex]a_{21} = 16[/latex].
For the following exercise, find the specified term given two terms from an arithmetic sequence.
- [latex]a_3 = -17.1[/latex] and [latex]a_{10} = -15.7[/latex]. Find [latex]a_{21}[/latex].
For the following exercise, use the recursive formula to write the first five terms of the arithmetic sequence.
- [latex]a_1 = -19[/latex]; [latex]a_n = a_{n-1} - 1.4[/latex]
For the following exercises, write a recursive formula for each arithmetic sequence.
- [latex]a = {17, \ 26, \ 35, \ \dots}[/latex]
- [latex]a = {12, \ 17, \ 22, \ \dots}[/latex]
- [latex]a = {8.9, \ 10.3, \ 11.7, \ \dots}[/latex]
- [latex]a = {\frac{1}{5}, \frac{9}{20}, \frac{7}{10}, \dots}[/latex]
- [latex]a = {\frac{1}{6}, -\frac{11}{12}, -2, \dots}[/latex]
For the following exercises, write a recursive formula for the given arithmetic sequence, and then find the specified term.
- [latex]a = {4, \ 11, \ 18, \ \dots}[/latex]; Find the [latex]14^{\text{th}}[/latex] term.
For the following exercises, use the explicit formula to write the first five terms of the arithmetic sequence.
- [latex]a_n = 24 - 4n[/latex]
For the following exercises, write an explicit formula for each arithmetic sequence.
- [latex]a = {3, 5, 7, \dots}[/latex]
- [latex]a = {-5, 95, 195, \dots}[/latex]
- [latex]a = {1.8, 3.6, 5.4, \dots}[/latex]
- [latex]a = {15.8, 18.5, 21.2, \dots}[/latex]
- [latex]a = {0, \frac{1}{3}, \frac{2}{3}, \dots}[/latex]
For the following exercises, find the number of terms in the given finite arithmetic sequence.
- [latex]a = {3, \ -4, \ -11, \ \dots, \ -60}[/latex]
- [latex]a = {\frac{1}{2}, \ 2, \ \frac{7}{2}, \ \dots, \ 8}[/latex]
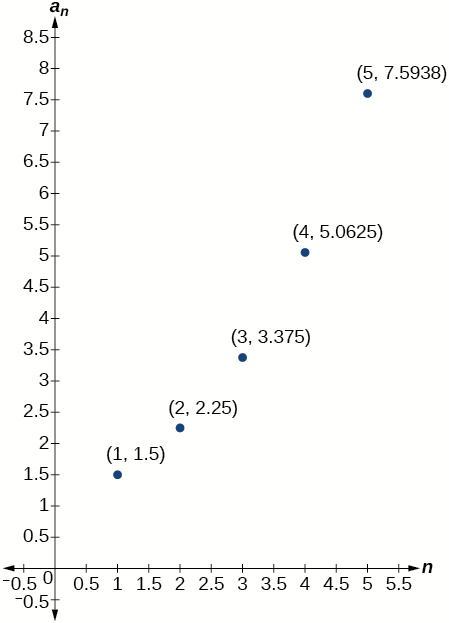
For the following exercise, determine whether the graph shown represents an arithmetic sequence.
For the following exercise, use the information provided to graph the first 5 terms of the arithmetic sequence.
- [latex]a_1 = 9; \quad a_n = a_{n-1} - 10[/latex]
Geometric Sequences
For the following exercise, find the common ratio for the geometric sequence.
- [latex]-0.125, \ 0.25, \ -0.5, \ 1, \ -2, \ \dots[/latex]
For the following exercises, determine whether the sequence is geometric. If so, find the common ratio.
- [latex]-6, \ -12, \ -24, \ -48, \ -96, \ \dots[/latex]
- [latex]-1, \ \frac{1}{2}, \ -\frac{1}{4}, \ \frac{1}{8}, \ -\frac{1}{16}, \ \dots[/latex]
- [latex]0.8, \ 4, \ 20, \ 100, \ 500, \ \dots[/latex]
For the following exercise, write the first five terms of the geometric sequence, given the first term and common ratio.
- [latex]a_1 = 5, \quad r = \frac{1}{5}[/latex]
For the following exercise, write the first five terms of the geometric sequence, given any two terms.
- [latex]a_6 = 25, \quad a_8 = 6.25[/latex]
For the following exercise, find the specified term for the geometric sequence, given the first term and common ratio.
- The first term is [latex]16[/latex], and the common ratio is [latex]-\frac{1}{3}[/latex]. Find the [latex]4^{\text{th}}[/latex] term.
For the following exercise, find the specified term for the geometric sequence, given the first four terms.
- [latex]a_n = {-2, \ \frac{2}{3}, \ -\frac{2}{9}, \ \frac{2}{27}, \ \dots }[/latex]. Find [latex]a_7[/latex].
For the following exercise, write the first five terms of the geometric sequence.
- [latex]a_1 = 7, \quad a_n = 0.2 , a_{n-1}[/latex]
For the following exercises, write a recursive formula for each geometric sequence.
- [latex]a_n = {-32, \ -16, \ -8, \ -4, \ \dots}[/latex]
- [latex]a_n = {10, \ -3, \ 0.9, \ -0.27, \ \dots}[/latex]
- [latex]a_n = {\frac{3}{5}, \ \frac{1}{10}, \ \frac{1}{60}, \ \frac{1}{360}, \ \dots}[/latex]
- [latex]a_n = {\frac{1}{512}, \ -\frac{1}{128}, \ \frac{1}{32}, \ -\frac{1}{8}, \ \dots}[/latex]
For the following exercise, write the first five terms of the geometric sequence.
- [latex]a_n = 12 \cdot \left(-\frac{1}{2}\right)^{n-1}[/latex]
For the following exercises, write an explicit formula for each geometric sequence.
- [latex]a_n = {1, \ 3, \ 9, \ 27, \ \dots}[/latex]
- [latex]a_n = {0.8, \ -4, \ 20, \ -100, \ \dots}[/latex]
- [latex]a_n = {-1, \ -\frac{4}{5}, \ -\frac{16}{25}, \ -\frac{64}{125}, \ \dots}[/latex]
- [latex]a_n = {3, \ 1, \ \frac{1}{3}, \ -\frac{1}{9}, \ \dots}[/latex]
For the following exercise, find the specified term for the geometric sequence given.
- Let [latex]a_n = -(-\frac{1}{3})^{n-1}[/latex]. Find [latex]a_{12}[/latex].
For the following exercises, find the number of terms in the given finite geometric sequence.
- [latex]a_n = {2, \ 1, \ \frac{1}{2}, \ \dots, \ \frac{1}{1024}}[/latex]
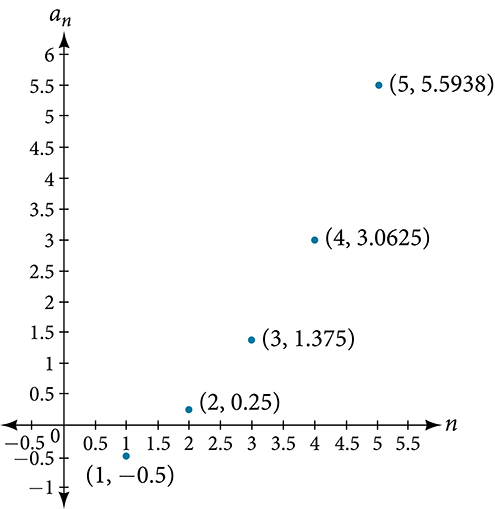
For the following exercise, determine whether the graph shown represents a geometric sequence.
For the following exercise, use the information provided to graph the first five terms of the geometric sequence.
- [latex]a_1 = 3, \quad a_n = 2a_{n-1}[/latex]
Series and Their Notations
For the following exercises, express each description of a sum using summation notation.
- The sum from [latex]n = 0[/latex] to [latex]n = 4[/latex] of [latex]5n[/latex]
- The sum that results from adding the number [latex]4[/latex] five times
For the following exercise, express each arithmetic sum using summation notation.
- [latex]10 + 18 + 26 + \dots + 162[/latex]
For the following exercises, use the formula for the sum of the first [latex]n[/latex] terms of each arithmetic sequence.
- [latex]\frac{3}{2} + 2 + \frac{5}{2} + 3 + \frac{7}{2}[/latex]
- [latex]3.2 + 3.4 + 3.6 + \dots + 5.6[/latex]
For the following exercises, express each geometric sum using summation notation.
- [latex]8 + 4 + 2 + \dots + 0.125[/latex]
For the following exercises, use the formula for the sum of the first [latex]n[/latex] terms of each geometric sequence, and then state the indicated sum.
- [latex]9 + 3 + 1 + \frac{1}{3} + \frac{1}{9}[/latex]
- [latex]\sum_{a=1}^{11} 64 \cdot 0.2^{a-1}[/latex]
For the following exercises, determine whether the infinite series has a sum. If so, write the formula for the sum. If not, state the reason.
- [latex]2 + 1.6 + 1.28 + 1.024 + \dots[/latex]
- [latex]\sum_{k=1}^{\infty} -\left(-\frac{1}{2}\right)^{k-1}[/latex]
For the following exercises, find the indicated sum.
- [latex]\sum_{n=1}^{6} n(n - 2)[/latex]
- [latex]\sum_{k=1}^{7} 2^k[/latex]
For the following exercises, use the formula for the sum of the first [latex]n[/latex] terms of an arithmetic series to find the sum.
- [latex]6 + \frac{15}{2} + 9 + \frac{21}{2} + 12 + \frac{27}{2} + 15[/latex]
- [latex]\sum_{k=1}^{11} \left(\frac{k}{2} - \frac{1}{2}\right)[/latex]
For the following exercise, use the formula for the sum of the first [latex]n[/latex] terms of a geometric series to find the partial sum.
- [latex]S_7[/latex] for the series [latex]0.4 - 2 + 10 - 50 \dots[/latex]
- [latex]\sum_{n=1}^{10} -2 \cdot \left(\frac{1}{2}\right)^{n-1}[/latex]
For the following exercises, find the sum of the infinite geometric series.
- [latex]-1 - \frac{1}{4} - \frac{1}{16} - \frac{1}{64} \dots[/latex]
- [latex]\sum_{n=1}^{\infty} 4.6 \cdot 0.5^{n-1}[/latex]
For the following exercises, determine the value of the annuity for the indicated monthly deposit amount, the number of deposits, and the interest rate.
- Deposit amount: [latex]$150[/latex]; total deposits: [latex]24[/latex]; interest rate: [latex]3 \%[/latex], compounded monthly
- Deposit amount: [latex]$100[/latex]; total deposits: [latex]120[/latex]; interest rate: [latex]10 \%[/latex], compounded semi-annually
Real-World Applications
- A boulder rolled down a mountain, traveling [latex]6[/latex] feet in the first second. Each successive second, its distance increased by [latex]8[/latex] feet. How far did the boulder travel after [latex]10[/latex] seconds?
- A pendulum travels a distance of [latex]3[/latex] feet on its first swing. On each successive swing, it travels [latex]\frac{3}{4}[/latex] the distance of the previous swing. What is the total distance traveled by the pendulum when it stops swinging?