Counting Principles
For the following exercises, determine whether to use the Addition Principle or the Multiplication Principle. Then perform the calculations.
- Let the set [latex]B={-23,-16,-7,-2,20,36,48,72}[/latex]. How many ways are there to choose a positive or an odd number from [latex]A[/latex]?
- How many ways are there to pick a paint color from [latex]5[/latex] shades of green, [latex]4[/latex] shades of blue, or [latex]7[/latex] shades of yellow?
- How many outcomes are possible from tossing a coin and rolling a 6-sided die?
- How many ways are there to construct a string of [latex]3[/latex] digits if numbers can be repeated?
For the following exercises, compute the value of the expression.
- [latex]P(5,2)[/latex]
- [latex]P(3,3)[/latex]
- [latex]P(11,5)[/latex]
- [latex]C(12,4)[/latex]
- [latex]C(7,6)[/latex]
For the following exercises, find the number of subsets in each given set.
- [latex]{1,2,3,4,5,6,7,8,9,10}[/latex]
- A set containing 5 distinct numbers, 4 distinct letters, and 3 distinct symbols
- The set of two-digit numbers between 1 and 100 containing the digit 0
For the following exercises, find the distinct number of arrangements.
- The letters in the word “academia”
- The symbols in the string #,#,#,@,@,$,$,$,%,%,%,%
Real-World Applications
- A cell phone company offers [latex]6[/latex] different voice packages and [latex]8[/latex] different data packages. Of those, [latex]3[/latex] packages include both voice and data. How many ways are there to choose either voice or data, but not both?
- A wholesale T-shirt company offers sizes small, medium, large, and extra-large in organic or non-organic cotton and colors white, black, gray, blue, and red. How many different T-shirts are there to choose from?
- An art store has [latex]4[/latex] brands of paint pens in [latex]12[/latex] different colors and [latex]3[/latex] types of ink. How many paint pens are there to choose from?
- How many ways can a baseball coach arrange the order of [latex]9[/latex] batters if there are [latex]15[/latex] players on the team?
- A motorcycle shop has [latex]10[/latex] choppers, [latex]6[/latex] bobbers, and [latex]5[/latex] café racers—different types of vintage motorcycles. How many ways can the shop choose [latex]3[/latex] choppers, [latex]5[/latex] bobbers, and [latex]2[/latex] café racers for a weekend showcase?
- Just-For-Kicks Sneaker Company offers an online customizing service. How many ways are there to design a custom pair of Just-For-Kicks sneakers if a customer can choose from a basic shoe up to [latex]11[/latex] customizable options?
- Suni bought [latex]20[/latex] plants to arrange along the border of her garden. How many distinct arrangements can she make if the plants are comprised of [latex]6[/latex] tulips, [latex]6[/latex] roses, and [latex]8[/latex] daisies?
Binomial Theorem
For the following exercises, evaluate the binomial coefficient.
- [latex]\begin{array}{c} 5 \\ 2 \end{array}[/latex]
- [latex]\begin{array}{c} 7 \\ 4 \end{array}[/latex]
- [latex]\begin{array}{c} 9 \\ 7 \end{array}[/latex]
- [latex]\begin{array}{c} 11 \\ 6 \end{array}[/latex]
For the following exercises, use the Binomial Theorem to expand each binomial.
- [latex](4a - b)^3[/latex]
- [latex](3a + 2b)^3[/latex]
- [latex](4x + 2y)^5[/latex]
- [latex](4x - 3y)^5[/latex]
- [latex](x^{-1} + 2y^{-1})^4[/latex]
For the following exercises, use the Binomial Theorem to write the first three terms of each binomial.
- [latex](a + b)^{17}[/latex]
- [latex](a - 2b)^{15}[/latex]
- [latex](3a + b)^{20}[/latex]
- [latex](x^3 - \sqrt{y})^8[/latex]
For the following exercises, find the indicated term of each binomial without fully expanding the binomial.
- The fourth term of [latex](3x - 2y)^5[/latex]
- The eighth term of [latex](7 + 5y)^{14}[/latex]
- The fifth term of [latex](x - y)^7[/latex]
- The ninth term of [latex](a - 3b^2)^{11}[/latex]
- The eighth term of [latex]\left(\frac{y}{2} + \frac{2}{x}\right)^9[/latex]
Introduction to Probability
https://openstax.org/books/college-algebra-corequisite-support-2e/pages/9-7-probability – Odd 7-49; 57-59
For the following exercises, use the spinner shown below to find the probabilities indicated.
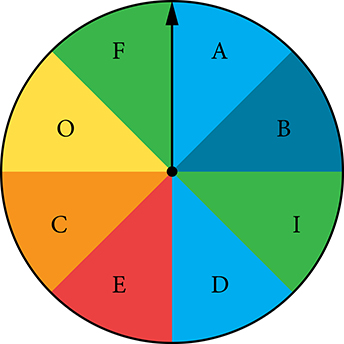
- Landing on a vowel
- Landing on purple or a vowel
- Landing on green or blue
- Not landing on yellow or a consonant
For the following exercises, two coins are tossed.
- Find the probability of tossing two heads.
- Find the probability of tossing at least one tail.
For the following exercises, four coins are tossed.
- Find the probability of tossing exactly two heads.
- Find the probability of tossing four heads or four tails.
- Find the probability of tossing not all tails.
- Find the probability of tossing either two heads or three heads.
For the following exercises, one card is drawn from a standard deck of 52 cards. Find the probability of drawing the following:
- A two
- Red six
- A non-ace
For the following exercises, two dice are rolled, and the results are summed.
- Construct a table showing the sample space of outcomes and sums.
- Find the probability of rolling at least one four or a sum of [latex]8[/latex].
- Find the probability of rolling a sum greater than or equal to [latex]15[/latex].
- Find the probability of rolling a sum less than [latex]6[/latex]or greater than [latex]9[/latex].
- Find the probability of rolling a sum of [latex]5[/latex] or [latex]6[/latex].
For the following exercises, a coin is tossed, and a card is pulled from a standard deck. Find the probability of the following:
- A head on the coin or a club
- A head on the coin or a face card
For the following exercises, use this scenario: a bag of M&Ms contains [latex]12[/latex] blue, [latex]6[/latex] brown, [latex]10[/latex] orange, [latex]8[/latex] yellow, [latex]8[/latex] red, and [latex]4[/latex] green M&Ms. Reaching into the bag, a person grabs [latex]5[/latex] M&Ms.
- What is the probability of getting all blue M&Ms?
- What is the probability of getting [latex]3[/latex]blue M&Ms?
Use this data for the exercises that follow: In 2020, there were roughly 331 million citizens in the United States, and about 55.8 million were elderly (aged 65 and over).
- If you meet five U.S. citizens, what is the percent chance that exactly one is elderly? (Round to the nearest tenth of a percent.)
- If you meet five U.S. citizens, what is the percent chance that four are elderly? (Round to the nearest thousandth of a percent.)