Properties of Real Numbers Cont.
Distributive Property
The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.
This property combines both addition and multiplication (and is the only property to do so).
distributive property
| Property | Example | In Words |
|---|---|---|
| Distributive Property [latex]a \times (b + c) = a \times b + a \times c[/latex] |
[latex]5 \times (3 + 4) = 5 \times 3 + 5 \times 4[/latex] | Multiplication distributes across addition |
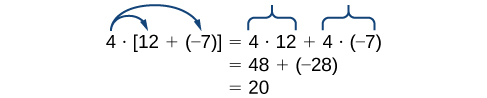
Note that [latex]4[/latex] is outside the grouping symbols, so we distribute the [latex]4[/latex] by multiplying it by [latex]12[/latex], multiplying it by [latex]–7[/latex], and adding the products.
To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.
Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.
For example, consider the difference [latex]12-\left(5+3\right)[/latex]. We can rewrite the difference of the two terms 12 and [latex]\left(5+3\right)[/latex] by turning the subtraction expression into addition of the opposite. So instead of subtracting [latex]\left(5+3\right)[/latex], we add the opposite.
Now, distribute [latex]-1[/latex] and simplify the result.
This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.
Identity Properties
The identity property of addition states that there is a unique number, called the additive identity ([latex]0[/latex]) that, when added to a number, results in the original number.
The identity property of multiplication states that there is a unique number, called the multiplicative identity ([latex]1[/latex]) that, when multiplied by a number, results in the original number.
identity properties
| Property | Example | In Words |
|---|---|---|
| Additive Identity Property [latex]a + 0 = a[/latex] |
[latex]17 + 0 = 17[/latex] | Any number plus [latex]0[/latex] is the number |
| Multiplicative Identity Property [latex]a \times 1 = a[/latex] |
[latex]21 \times 1 = 21[/latex] | Any number times one is the number |
There are no exceptions for these properties; they work for every real number, including [latex]0[/latex] and [latex]1[/latex].
Inverse Properties
The inverse property of addition states that, for every real number a, there is a unique number, called the additive inverse (or opposite), denoted−a, that, when added to the original number, results in the additive identity, 0.
For example, if [latex]a=-8[/latex], the additive inverse is 8, since [latex]\left(-8\right)+8=0[/latex].
The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a, there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\frac{1}{a}[/latex], that, when multiplied by the original number, results in the multiplicative identity, 1.
For example, if [latex]a=-\frac{2}{3}[/latex], the reciprocal, denoted [latex]\frac{1}{a}[/latex], is [latex]-\frac{3}{2}[/latex] because
inverse properties
| Property | Example | In Words |
|---|---|---|
| Additive Inverse Property [latex]a + (-a) = 0[/latex] |
[latex]14 + (-14) = 0[/latex] | Every number plus its negative is [latex]0[/latex] |
| Multiplicative Inverse Property [latex]a \times \frac{1}{a} = 1[/latex], provided [latex](a \neq 0)[/latex] |
[latex]3 \times \frac{1}{3} = 1[/latex] | Every non-zero number times its reciprocal is [latex]1[/latex] |
- [latex]3\cdot 6+3\cdot 4[/latex]
- [latex]\left(5+8\right)+\left(-8\right)[/latex]
- [latex]6-\left(15+9\right)[/latex]
- [latex]\dfrac{4}{7}\cdot \left(\frac{2}{3}\cdot \dfrac{7}{4}\right)[/latex]
- [latex]100\cdot \left[0.75+\left(-2.38\right)\right][/latex]