Introduction to Power and Polynomial Functions
For the following exercises, identify the function as a power function, a polynomial function, or neither.
- [latex]f(x)=(x^2)^3[/latex]
- [latex]f(x)=\frac{x^2}{x^2−1}[/latex]
- [latex]f(x)=3^{x+1}[/latex]
For the following exercises, find the degree and leading coefficient for the given polynomial.
- [latex]7−2x^2[/latex]
- [latex]x(4−x^2)(2x+1)[/latex]
For the following exercises, determine the end behavior of the functions.
- [latex]f(x)=x^4[/latex]
- [latex]f(x)=−x^4[/latex]
- [latex]f(x)=−2x^4−3x^2+x−1[/latex]
- [latex]f(x)=x^2(2x^3-x+1)[/latex]
For the following exercises, find the intercepts of the functions.
- [latex]f(t)=2(t−1)(t+2)(t−3)[/latex]
- [latex]f(x)=x^4−16[/latex]
- [latex]f(x)=x(x^2−2x−8)[/latex]
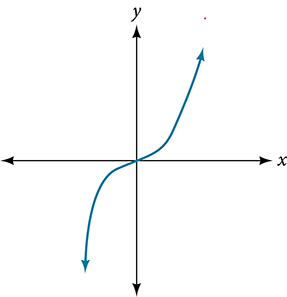
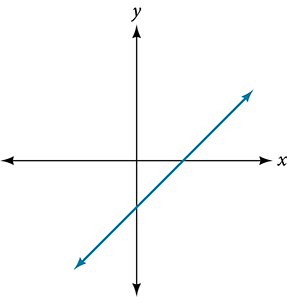
For the following exercises, determine the least possible degree of the polynomial function shown.
For the following exercises, determine whether the graph of the function provided is a graph of a polynomial function. If so, determine the number of turning points and the least possible degree for the function.
- [latex]V(m)=(3+2m)^3[/latex], where [latex]m[/latex] is the number of minutes elapsed.
- [latex]V(x)=x(8-2x)^2[/latex], where [latex]x[/latex] is the length of the square’s side in inches.
Graphs of Polynomial Functions
For the following exercises, find the [latex]x[/latex]– or [latex]t[/latex]-intercepts of the polynomial functions.
- [latex]C(t)=3(t+2)(t−3)(t+5)[/latex]
- [latex]C(t)=2t(t−3)(t+1)^2[/latex]
- [latex]C(t)=4t^4+12t^3−40t^2[/latex]
- [latex]f(x)=x^3+x^2−20x[/latex]
- [latex]f(x)=x^3+x^2−4x-4[/latex]
- [latex]f(x)=2x^3-x^2−8x+4[/latex]
- [latex]f(x)=2x^4+6x^2-8[/latex]
- [latex]f(x)=x^6-2x^4-3x^2[/latex]
- [latex]f(x)=x^5-5x^3+4x[/latex]
For the following exercises, use the Intermediate Value Theorem to confirm that the given polynomial has at least one zero within the given interval.
- [latex]f(x)=x^3−9x[/latex], between [latex]x=2[/latex] and [latex]x=4[/latex].
- [latex]f(x)=−x^4+4[/latex], between [latex]x=1[/latex] and [latex]x=3[/latex].
- [latex]f(x)=x^3−100x+2[/latex], between [latex]x=0.01[/latex] and [latex]x=0.1[/latex].
For the following exercises, find the zeros and give the multiplicity of each.
- [latex]f(x)=x^2(2x+3)^5(x−4)^2[/latex]
- [latex]f(x)=x^2(x^2+4x+4)[/latex]
- [latex]f(x)=(3x+2)^5(x^2−10x+25)[/latex]
- [latex]f(x)=x^6-x^5-2x^4[/latex]
- [latex]f(x)=4x^5-12x^4+9x^3[/latex]
- [latex]f(x)=4x^4(9x^4-12x^3+4x^2)[/latex]
For the following exercises, graph the polynomial functions. Note [latex]x[/latex]– and [latex]y[/latex]– intercepts, multiplicity, and end behavior.
- [latex]g(x)=(x+4)(x−1)^2[/latex]
- [latex]k(x)=(x−3)^3(x−2)^2[/latex]
- [latex]n(x)=−3x(x+2)(x−4)[/latex]
For the following exercises, use the graphs to write the formula for a polynomial function of least degree.
For the following exercises, use the graph to identify zeros and multiplicity.
For the following exercises, use the given information about the polynomial graph to write the equation.
- Degree [latex]3[/latex]. Zeros at [latex]x=–2, x=1[/latex], and [latex]x=3[/latex]. [latex]y[/latex]-intercept at [latex](0,–4)[/latex].
- Degree [latex]5[/latex]. Roots of multiplicity [latex]2[/latex] at [latex]x=3[/latex] and [latex]x=1[/latex], and a root of multiplicity [latex]1[/latex] at [latex]x=–3[/latex]. [latex]y[/latex]-intercept at [latex](0,9)[/latex].
- Degree [latex]5[/latex]. Double zero at [latex]x=1[/latex], and triple zero at [latex]x=3[/latex]. Passes through the point [latex](2,15)[/latex].
- Degree 3. Zeros at [latex]x=-3[/latex], [latex]x=-2[/latex] and [latex]x=1[/latex]. y-intercept at [latex](0,12)[/latex].
- Degree 4. Roots of multiplicity 2 at [latex]x=\dfrac{1}{2}[/latex] and roots of multiplicity 1 at [latex]x=6[/latex] and [latex]x=-2[/latex]. y-intercept at [latex](0,18)[/latex].
Dividing Polynomials
For the following exercises, use long division to divide. Specify the quotient and the remainder.
- [latex](x^2+5x−1)÷(x−1)[/latex]
- [latex](3x^2+23x+14)÷(x+7)[/latex]
- [latex](6x^2−25x−25)÷(6x+5)[/latex]
- [latex](2x^2−3x+2)÷(x+2)[/latex]
For the following exercises, use synthetic division to find the quotient. Ensure the equation is in the form required by synthetic division. (Hint: divide the dividend and divisor by the coefficient of the linear term in the divisor.)
- [latex](2x^3−6x^2−7x+6)÷(x−4)[/latex]
- [latex](4x^3−12x^2−5x−1)÷(2x+1)[/latex]
- [latex](3x^3−2x^2+x−4)÷(x+3)[/latex]
- [latex](2x^3+7x^2−13x−3)÷(2x−3)[/latex]
- [latex](4x^3-5x^2+13)÷(x+4)[/latex]
- [latex](x^3-21x^2+147x−343)÷(x-7)[/latex]
For the following exercises, use synthetic division to determine whether the first expression is a factor of the second. If it is, indicate the factorization.
- [latex]x−2[/latex], [latex]3x^4−6x^3−5x+10[/latex]
- [latex]x−2[/latex], [latex]4x^4−15x^2−4[/latex]
- [latex]x+\frac{1}{3}[/latex], [latex]3x^4+x^3−3x+1[/latex]
Zeros of Polynomial Functions
For the following exercises, use the Remainder Theorem to find the remainder.
- [latex](3x^3−2x^2+x−4)÷(x+3)[/latex]
- [latex](−3x^2+6x+24)÷(x−4)[/latex]
- [latex](x^4−1)÷(x−4)[/latex]
- [latex](4x^3+5x^2−2x+7)÷(x+2)[/latex]
For the following exercises, use the given factor and the Factor Theorem to find all real zeros for the given polynomial function.
- [latex]f(x)=2x^3+x^2−5x+2; x+2[/latex]
- [latex]f(x)=2x^3+3x^2+x+6; x+2[/latex]
- [latex]x^3+3x^2+4x+12; x+3[/latex]
- [latex]2x^3+5x^2−12x−30; 2x+5[/latex]
For the following exercises, use the Rational Zero Theorem to find the real solution(s) to each equation.
- [latex]2x^3+7x^2−10x−24=0[/latex]
- [latex]x^3+5x^2−16x−80=0[/latex]
- [latex]2x^3−3x^2−32x−15=0[/latex]
- [latex]2x^3−3x^2−x+1=0[/latex]
- [latex]2x^3−5x^2+9x-9=0[/latex]
For the following exercises, find all complex solutions (real and non-real).
- [latex]x^3-8x^2+25x-26=0[/latex] Solutions: [latex]x=2[/latex], [latex]x=3\pm i[/latex]
- [latex]3x^3-4x^2+11x+10=0[/latex] Solutions: [latex]x=-1[/latex], [latex]x=\dfrac{2\pm i\sqrt{11}}{3}[/latex]
- [latex]2x^3-3x^2+32x+17=0[/latex] Solutions: [latex]x=-1[/latex], [latex]x=2\pm2i[/latex]
For the following exercises, use Descartes’ Rule to determine the possible number of positive and negative solutions. Confirm with the given graph.
- [latex]f(x)=x^4-x^2-1[/latex]
- [latex]f(x)=x^3-2x^2+x-1[/latex]
- [latex]f(x)=2x^3+37x^2+200x+300[/latex]
- [latex]f(x)=2x^4-5x^3-5x^2+5x+3[/latex]
- [latex]f(x)=10x^4-21x^2+11[/latex]
For the following exercises, list all possible rational zeros for the functions.
- [latex]f(x)=2x^3+3x^2−8x+5[/latex]
- [latex]f(x)=6x^4−10x^2+13x+1[/latex]
For the following exercises, find the dimensions of the box described.
- The length is twice as long as the width. The height is [latex]2[/latex] inches greater than the width. The volume is [latex]192[/latex] cubic inches.
- The length is one inch more than the width, which is one inch more than the height. The volume is [latex]86.625[/latex] cubic inches.
- The length is [latex]3[/latex] inches more than the width. The width is [latex]2[/latex] inches more than the height. The volume is [latex]120[/latex] cubic inches.
For the following exercises, find the dimensions of the right circular cylinder described.
- The height is one less than one half the radius. The volume is [latex]72\pi[/latex] cubic meters.
- The radius and height differ by two meters. The height is greater and the volume is [latex]28.125\pi[/latex] cubic meters.