Quadratic Functions: Get Stronger

Introduction to Quadratic Functions and Parabolas

For the following exercises, rewrite the quadratic functions in standard form and give the vertex.

  1. [latex]g(x)=x^2+2x−3[/latex]
  2. [latex]f(x)=x^2+5x−2[/latex]
  3. [latex]k(x)=3x^2−6x−9[/latex]
  4. [latex]f(x)=3x^2-5x-1[/latex]

For the following exercises, determine whether there is a minimum or maximum value to each quadratic function. Find the value and the axis of symmetry.

  1. [latex]f(x)=2x^2−10x+4[/latex]
  2. [latex]f(x)=4x^2+x−1[/latex]
  3. [latex]f(x)=\frac{1}{2}x^2+3x+1[/latex]

For the following exercises, determine the domain and range of the quadratic function.

  1. [latex]f(x)=(x−3)^2+2[/latex]
  2. [latex]f(x)=x^2+6x+4[/latex]
  3. [latex]k(x)=3x^2−6x−9[/latex]

For the following exercises, use the vertex [latex](h,k)[/latex] and a point on the graph [latex](x,y)[/latex] to find the general form of the equation of the quadratic function.

  1. [latex](h,k)=(−2,−1),(x,y)=(−4,3)[/latex]
  2. [latex](h,k)=(2,3),(x,y)=(5,12)[/latex]
  3. [latex](h,k)=(3,2),(x,y)=(10,1)[/latex]
  4. [latex](h,k)=(1,0),(x,y)=(0,1)[/latex]

For the following exercises, sketch a graph of the quadratic function and give the vertex, axis of symmetry, and intercepts.

  1. [latex]f(x)=x^2−6x−1[/latex]
  2. [latex]f(x)=x^2−7x+3[/latex]
  3. [latex]f(x)=4x^2−12x−3[/latex]

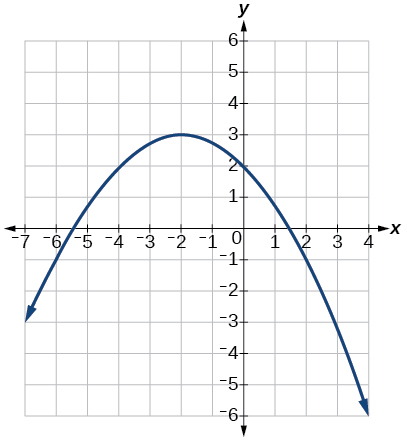
For the following exercises, write the equation for the graphed quadratic function.

  1. Graph of a positive parabola with a vertex at (-1, 2) and y-intercept at (0, 3)
  2. Graph of a negative parabola with a vertex at (-1, 2).
  3. Graph of a negative parabola with a vertex at (-2, 3).

Complex Numbers and Operations

For the following exercises, plot each number in the complex plane.

  1. [latex]4[/latex]
  2. [latex]–3i[/latex]
  3. [latex]–2+3i[/latex]
  4. [latex]2 + i[/latex]
  5. [latex]-2[/latex]
  6. [latex]4i[/latex]
  7. [latex]1+2i[/latex]
  8. [latex]-1-i[/latex]

For the following exercises, solve.

  1. [latex](2+3i) + (3-4i)[/latex]
  2. [latex](3-5i) - (-2-i)[/latex]
  3. [latex](1-i) + (2+4i)[/latex]
  4. [latex]( -2-3i) - (4-2i)[/latex]

For the following exercises, multiply the expressions.

  1. latex]3(2+4i)[/latex]
  2. [latex](2i)(-1-5i)[/latex]
  3. [latex](2-4i)(1+3i)[/latex]
  4. [latex]2(-1+3i)[/latex]
  5. [latex](3i)(2-6i)[/latex]
  6. [latex](1-i)(2+5i)[/latex]

 

  1. Plot the number [latex]2+3i[/latex]. Does multiplying by [latex]1-i[/latex] move the point closer to or further from the origin? Does it rotate the point, and if so which direction?
  2. Plot the number [latex]2+3i[/latex]. Does multiplying by [latex]0.75+0.5i[/latex] move the point closer to or further from the origin? Does it rotate the point, and if so which direction.

Application of Quadratic Functions

  1. Suppose that the price per unit in dollars of a cell phone production is modeled by [latex]p=$45-0.0125x[/latex], where [latex]x[/latex] is in thousands of phones produced, and the revenue represented by thousands of dollars is [latex]R=x\cdot p[/latex]. Find the production level that will maximize revenue.
  2. A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by [latex]h(t)=-4.9t^2+24t+8[/latex]. How long does it take to reach maximum height?
  3. A farmer finds that if she plants [latex]75[/latex] trees per acre, each tree will yield [latex]20[/latex] bushels of fruit. She estimates that for each additional tree planted per acre, the yield of each tree will decrease by [latex]3[/latex] bushels. How many trees should she plant per acre to maximize her harvest?