Introduction to Functions

For the following exercises, determine whether the relation represents [latex]y[/latex] as a function of [latex]x[/latex].

1. [latex]y = x^2[/latex]
2. [latex]3 - \sqrt{6-2x}[/latex]
3. [latex]3x^2 + y = 14[/latex]
4. [latex]y = -2x^2 + 40x[/latex]
5. [latex]x = \dfrac{3y + 5}{7y - 1}[/latex]
6. [latex]y = \dfrac{3x + 5}{7x - 1}[/latex]
7. [latex]2xy = 1[/latex]
8. [latex]y = x^3[/latex]
9. [latex]x = \pm \sqrt{1 - y}[/latex]
10. [latex]y^2 = x^2[/latex]

For the following exercises, evaluate [latex]f(-3)[/latex], [latex]f(2)[/latex], [latex]f(-a)[/latex], [latex]-f(a)[/latex], [latex]f(a + h)[/latex].

11. [latex]f(x) = 2x - 5[/latex]
12. [latex]f(x) = \sqrt{2 - x + 5}[/latex]
13. [latex]f(x) = |x - 1| - |x + 1|[/latex]
14. Given the function [latex]g(x) = x^2 + 2x[/latex], evaluate [latex]\dfrac{g(x) - g(a)}{x - a}[/latex], [latex]x \neq a[/latex].
15. Given the function [latex]f(x) = 8 - 3x[/latex]:
    1. Evaluate [latex]f(-2)[/latex].
    2. Solve [latex]f(x) = -1[/latex].
16. Given the function [latex]f(x) = x^2 - 3x[/latex]:
    1. Evaluate [latex]f(5)[/latex].
    2. Solve [latex]f(x) = 4[/latex].

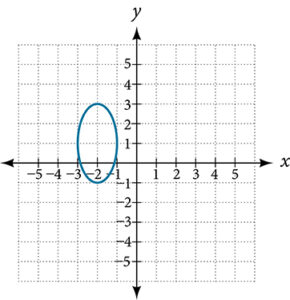
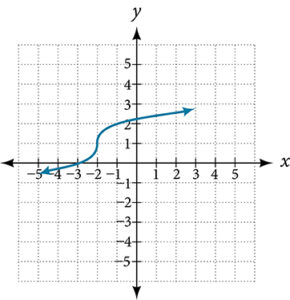
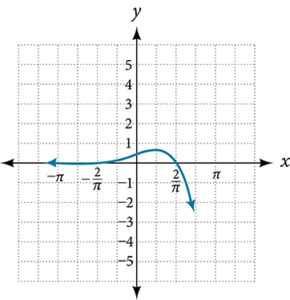
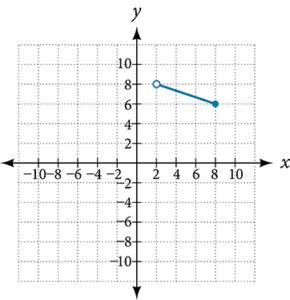
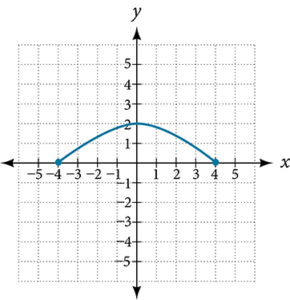
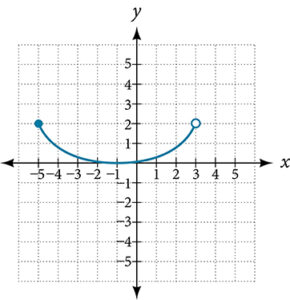
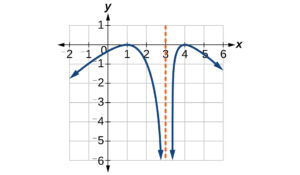
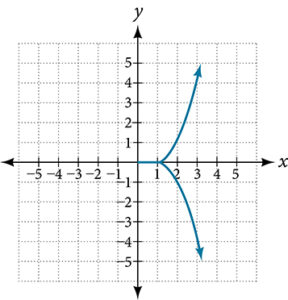
For the following exercises, use the vertical line test to determine which graphs show relations that are functions.

21. 
22. 
23. 
24. 
25. 
26. 
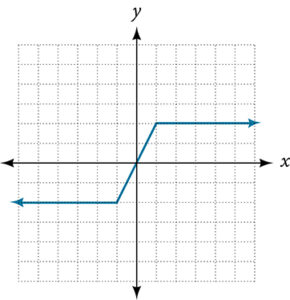
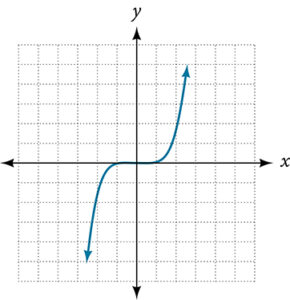
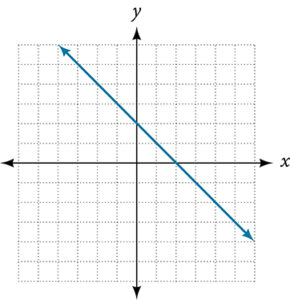
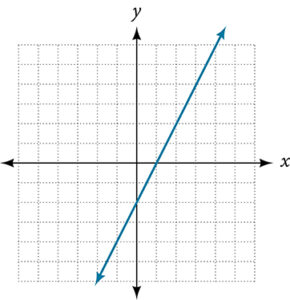
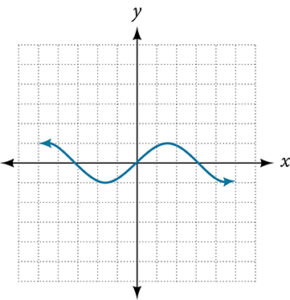
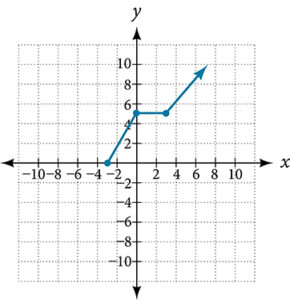
27. Given the following graph,
    
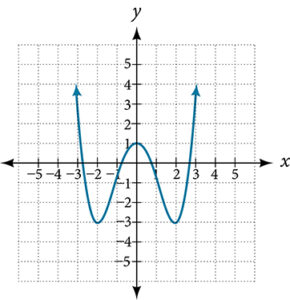
    1. Evaluate [latex]f(0)[/latex].
    2. Solve for [latex]f(x) = -3[/latex].

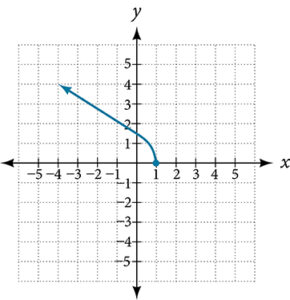
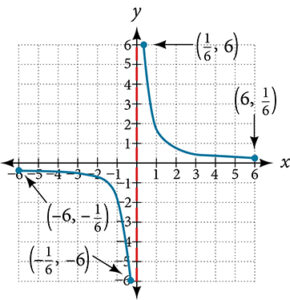
For the following exercises, determine if the given graph is a one-to-one function.

30. 
31. 
32. 

For the following exercise, determine whether the relation represents a function.

33. [latex]\{(3, 4), (4, 5), (5, 6)\}[/latex]

For the following exercises, determine if the relation represented in table form represents [latex]y[/latex] as a function of [latex]x[/latex].

34. [latex]x[/latex]	[latex]5[/latex]	[latex]10[/latex]	[latex]15[/latex]
    [latex]y[/latex]	[latex]3[/latex]	[latex]8[/latex]	[latex]14[/latex]

35. [latex]x[/latex]	[latex]5[/latex]	[latex]10[/latex]	[latex]10[/latex]
    [latex]y[/latex]	[latex]3[/latex]	[latex]8[/latex]	[latex]14[/latex]

For the following exercises, use the function [latex]f[/latex] represented in the table below.

[latex]x[/latex]	[latex]0[/latex]	[latex]1[/latex]	[latex]2[/latex]	[latex]3[/latex]	[latex]4[/latex]	[latex]5[/latex]	[latex]6[/latex]	[latex]7[/latex]	[latex]8[/latex]	[latex]9[/latex]
[latex]f(x)[/latex]	[latex]74[/latex]	[latex]28[/latex]	[latex]1[/latex]	[latex]53[/latex]	[latex]56[/latex]	[latex]3[/latex]	[latex]36[/latex]	[latex]45[/latex]	[latex]14[/latex]	[latex]47[/latex]

36. Solve [latex]f(x) = 1[/latex].

37. The number of cubic yards of dirt, [latex]D[/latex], needed to cover a garden with area [latex]a[/latex] square feet is given by [latex]D = g(a)[/latex].
    1. A garden with area [latex]5000 \, \text{ft}^2[/latex] requires [latex]50 \, \text{yd}^3[/latex] of dirt. Express this information in terms of the function [latex]g[/latex].
    2. Explain the meaning of the statement [latex]g(100) = 1[/latex].
38. Let [latex]h(t)[/latex] be the height above ground, in feet, of a rocket [latex]t[/latex] seconds after launching. Explain the meaning of each statement:
    1. [latex]h(1) = 200[/latex]
    2. [latex]h(2) = 350[/latex]

Domain and Range

For the following exercises, find the domain of each function using interval notation.

1. [latex]f(x) = 5 - 2x^2[/latex]
2. [latex]f(x) = \sqrt{x^2 + 4}[/latex]
3. [latex]f(x) = \sqrt[3]{x-1}[/latex]
4. [latex]f(x) = \dfrac{3x + 1}{4x + 2}[/latex]
5. [latex]f(x) = \dfrac{x - 3}{x^2 + 9x - 22}[/latex]
6. [latex]f(x) = \dfrac{2x^3 - 250}{x^2 - 2x - 15}[/latex]
7. [latex]f(x) = \dfrac{2x + 1}{\sqrt{5 - x}}[/latex]
8. [latex]f(x) = \dfrac{\sqrt{x - 6}}{\sqrt{x - 4}}[/latex]
9. [latex]f(x) = \dfrac{x^2 - 9x}{x^2 - 81}[/latex]

For the following exercises, write the domain and range of each function using interval notation.

10. 
11. 
12. 
13. 
14. 
15. 

For the following exercises, sketch a graph of the piecewise function. Write the domain in interval notation.

16. [latex]f(x) = \begin{cases} 2x - 1 & \text{if } x < 1 \\ 1 + x & \text{if } x \geq 1 \end{cases}[/latex]
17. [latex]f(x) = \begin{cases} 3 & \text{if } x < 0 \\ \sqrt{x} & \text{if } x \geq 0 \end{cases}[/latex]
18. [latex]f(x) = \begin{cases} x^2 & \text{if } x < 0 \\ x + 2 & \text{if } x \geq 0 \end{cases}[/latex]
19. [latex]f(x) = \begin{cases} |x| & \text{if } x < 2 \\ 1 & \text{if } x \geq 2 \end{cases}[/latex]

For the following exercise, given each function [latex]f[/latex], evaluate [latex]f(-3)[/latex], [latex]f(-2)[/latex], [latex]f(-1)[/latex], and [latex]f(0)[/latex].

20. [latex]f(x) = \begin{cases} 1 & \text{if } x \leq -3 \\ 0 & \text{if } x > -3 \end{cases}[/latex]

For the following exercises, given each function [latex]f[/latex], evaluate [latex]f(-1)[/latex], [latex]f(0)[/latex], [latex]f(2)[/latex], and [latex]f(4)[/latex].

21. [latex]f(x) = \begin{cases} 7x + 3 & \text{if } x < 0 \\ 7x + 6 & \text{if } x \geq 0 \end{cases}[/latex]
22. [latex]f(x) = \begin{cases} 5x & \text{if } x < 0 \\ 3 & \text{if } 0 \leq x \leq 3 \\ x^2 & \text{if } x > 3 \end{cases}[/latex]

For the following exercise, write the domain for the piecewise function in interval notation.

23. [latex]f(x) = \begin{cases} x^2 - 2 & \text{if } x < 1 \\ -x^2 + 2 & \text{if } x \geq 1 \end{cases}[/latex]

Rates of Change and Behavior of Graphs

For the following exercises, find the average rate of change of each function on the interval specified for real numbers [latex]b[/latex] or [latex]h[/latex] in simplest form.

1. [latex]f(x) = 2x^2 + 1[/latex] on [latex][x, x + h][/latex]
2. [latex]a(t) = \dfrac{1}{t + 4}[/latex] on [latex][9, 9 + h][/latex]
3. [latex]j(x) = 3x^3[/latex] on [latex][1, 1 + h][/latex]
4. Find [latex]\dfrac{f(x+h)-f(x)}{h}[/latex] given [latex]f(x) = 2x^2 - 3x[/latex] on [latex][x, x + h][/latex]

For the following exercise, consider the graph of [latex]f[/latex] shown in the figure below.

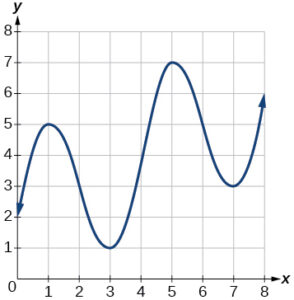
5. Estimate the average rate of change from [latex]x = 2[/latex] to [latex]x = 5[/latex].

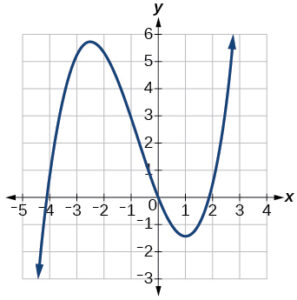
For the following exercises, use the graph of each function to estimate the intervals on which the function is increasing or decreasing.

6. 
7. 

For the following exercises, find the average rate of change of each function on the interval specified.

8. [latex]h(x) = 5 - 2x^2[/latex] on [latex][-2, 4][/latex]
9. [latex]g(x) = 3x^3 - 1[/latex] on [latex][-3, 3][/latex]
10. [latex]p(t) = \dfrac{(t^2 - 4)(t + 1)}{t^2 + 3}[/latex] on [latex][-3, 1][/latex]

Real-World Applications.

11. A driver of a car stopped at a gas station to fill up their gas tank. They looked at their watch, and the time read exactly 3:40 p.m. At this time, they started pumping gas into the tank. At exactly 3:44, the tank was full and the driver noticed that they had pumped [latex]10.7[/latex] gallons. What is the average rate of flow of the gasoline into the gas tank?
12. The graph below illustrates the decay of a radioactive substance over [latex]t[/latex] days.
    
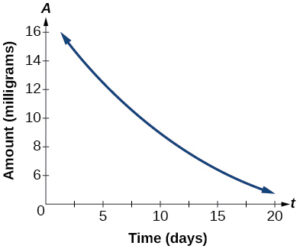
    Use the graph to estimate the average decay rate from [latex]t = 5[/latex] to [latex]t = 15[/latex].