Absolute Value Inequalities
An absolute value inequality is an equation of the form
where A, and sometimes B, represents an algebraic expression dependent on a variable x. Solving the inequality means finding the set of all [latex]x[/latex] –values that satisfy the problem. Usually this set will be an interval or the union of two intervals and will include a range of values.
absolute value inequality
For an algebraic expression [latex]X[/latex] and [latex]k>0[/latex], an absolute value inequality is an inequality of the form:
These statements also apply to [latex]|X|\le k[/latex] and [latex]|X|\ge k[/latex].
There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two equations. The advantage of the algebraic approach is that solutions are exact, as precise solutions are sometimes difficult to read from a graph.
We can solve algebraically for the set of [latex]x-[/latex]values such that the distance between [latex]x[/latex] and [latex]600[/latex] is less than [latex]200[/latex]. We represent the distance between [latex]x[/latex] and [latex]600[/latex] as [latex]|x - 600|[/latex], and therefore,
This means our returns would be between [latex]$400[/latex] and [latex]$800[/latex].
To solve absolute value inequalities, just as with absolute value equations, we write two inequalities and then solve them independently.

We want the distance between [latex]x[/latex] and [latex]5[/latex] to be less than or equal to [latex]4[/latex]. We can draw a number line to represent the condition to be satisfied.The distance from [latex]x[/latex] to [latex]5[/latex] can be represented using an absolute value symbol, [latex]|x - 5|[/latex]. Write the values of [latex]x[/latex] that satisfy the condition as an absolute value inequality.
We need to write two inequalities as there are always two solutions to an absolute value equation.
If the solution set is [latex]x\le 9[/latex] and [latex]x\ge 1[/latex], then the solution set is an interval including all real numbers between and including [latex]1[/latex] and [latex]9[/latex].
So, [latex]|x - 5|\le 4[/latex] is equivalent to [latex]\left[1,9\right][/latex] in interval notation.
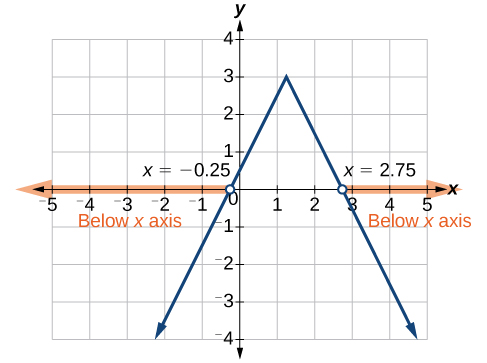
determine the [latex]x[/latex]-values for which the [latex]y[/latex]-values are negative.
Sometimes a picture is worth a thousand words. You can turn a single variable inequality into a two variable inequality and make a graph. The [latex]x[/latex]-intercepts of the graph will correspond with the solution to the inequality you can find by hand.
When solving [latex]-2|k - 4|\le -6[/latex] we can change the variable to [latex]x[/latex] to make it easier to enter in an online graphing calculator.
To turn [latex]-2|x - 4|\le -6[/latex] into a two variable equation, move everything to one side, and place the variable y on the other side like this:
[latex]-2|x - 4|\le -6[/latex]
[latex]-2|x - 4|+6\le y[/latex]
Now enter this inequality in an online graphing calculator and hover over the [latex]x[/latex]-intercepts.
If you need instruction on how to enter inequalities in an online graphing calculator, watch this tutorial for the process within Desmos. Other calculators will behave slightly differently.
You can view the transcript for “Learn Desmos: Inequalities” here (opens in new window).
Are the x-values of the intercepts the same values as the solution we found above?
Now you try turning this single variable inequality into a two variable inequality:
[latex]5|9-2x|\ge10[/latex]
Graph your inequality with an online graphing calculator, and write the solution interval.