Quadratic Equations
For the following exercises, solve the quadratic equation by factoring.
- [latex]x^2 - 9x + 18 = 0[/latex]
- [latex]6x^2 + 17x + 5 = 0[/latex]
- [latex]3x^2 - 75 = 0[/latex]
- [latex]4x^2 = 9[/latex]
- [latex]5x^2 = 5x + 30[/latex]
- [latex]7x^2 + 3x = 0[/latex]
For the following exercises, solve the quadratic equation by using the square root property.
- [latex]x^2 = 36[/latex]
- [latex](x-1)^2 = 25[/latex]
- [latex](2x+1)^2 = 9[/latex]
For the following exercises, solve the quadratic equation by completing the square. Show each step.
- [latex]x^2 - 9x - 22 = 0[/latex]
- [latex]x^2 - 6x = 13[/latex]
- [latex]2 + z = 6z^2[/latex]
- [latex]2x^2 - 3x - 1 = 0[/latex]
For the following exercises, determine the discriminant, and then state how many solutions there are and the nature of the solutions. Do not solve.
- [latex]x^2 + 4x + 7 = 0[/latex]
- [latex]9x^2 - 30x + 25 = 0[/latex]
- [latex]6x^2 - x - 2 = 0[/latex]
For the following exercises, solve the quadratic equation by using the quadratic formula. If the solutions are not real, state No Real Solution.
- [latex]x^2 + x = 4[/latex]
- [latex]3x^2 - 5x + 1 = 0[/latex]
- [latex]4 + \dfrac{1}{x} - \dfrac{1}{x^2} = 0[/latex]
Extensions
- Beginning with the general form of a quadratic equation, [latex]ax^2 + bx + c = 0[/latex], solve for x by using the completing the square method, thus deriving the quadratic formula.
- A person has a garden that has a length [latex]10[/latex] feet longer than the width. Set up a quadratic equation to find the dimensions of the garden if its area is [latex]119[/latex] ft[latex]^2[/latex]. Solve the quadratic equation to find the length and width.
- Suppose that an equation is given [latex]p = -2x^2 + 280x - 1000[/latex], where x represents the number of items sold at an auction and p is the profit made by the business that ran the auction. How many items sold would make this profit a maximum? Solve this by graphing the expression in your graphing utility and finding the maximum using 2[latex]^{\text{nd}}[/latex] CALC maximum. To obtain a good window for the curve, set [latex]x[/latex] [latex][0,200][/latex]and [latex]y[/latex] [latex][0,10000][/latex].
Real-World Applications
- The cost function for a certain company is [latex]C = 60x + 300[/latex] and the revenue is given by [latex]R = 100x - 0.5x^2[/latex]. Recall that profit is revenue minus cost. Set up a quadratic equation and find two values of [latex]x[/latex] (production level) that will create a profit of [latex]$300[/latex].
- A vacant lot is being converted into a community garden. The garden and the walkway around its perimeter have an area of [latex]378[/latex] ft[latex]^2[/latex]. Find the width of the walkway if the garden is [latex]12[/latex] ft. wide by [latex]15[/latex] ft. long.
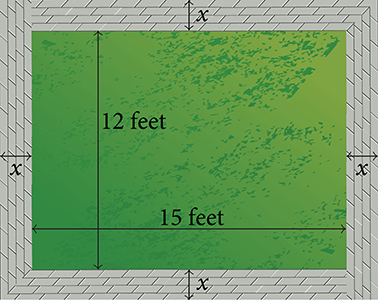
Lot enclosed by walls with labels
Other Types of Equations
For the following exercises, solve each rational equation for x. State all x-values that are excluded from the solution set.
- [latex]\dfrac{3}{x} - \dfrac{1}{3} = \dfrac{1}{6}[/latex]
- [latex]\dfrac{3}{x-2} - \dfrac{1}{x-1} + \dfrac{7}{(x-1)(x-2)}[/latex]
- [latex]\dfrac{1}{x} = \dfrac{1}{5} + \dfrac{3}{2x}[/latex]
For the following exercises, solve the rational exponent equation. Use factoring where necessary.
- [latex]x^{\dfrac{3}{4}} = 27[/latex]
- [latex](x-1)^{\dfrac{3}{4}} = 8[/latex]
- [latex]x^{\dfrac{2}{3}} - 5x^{\dfrac{1}{3}} + 6 = 0[/latex]
For the following exercises, solve the following polynomial equations by grouping and factoring.
- [latex]x^3 + 2x^2 - x - 2 = 0[/latex]
- [latex]4y^3 - 9y = 0[/latex]
- [latex]m^3 + m^2 - m - 1 = 0[/latex]
- [latex]5x^3 + 45x = 2x^2 + 18[/latex]
For the following exercises, solve the radical equation. Be sure to check all solutions to eliminate extraneous solutions.
- [latex]\sqrt{x - 7} = 5[/latex]
- [latex]\sqrt{3t + 5} = 7[/latex]
- [latex]\sqrt{12 - x} = x[/latex]
- [latex]\sqrt{3x + 7} + \sqrt{x + 2} = 1[/latex]
For the following exercises, solve the equation involving absolute value.
- [latex]|3x - 4| = 8[/latex]
- [latex]|1 - 4x| - 1 = 5[/latex]
- [latex]|2x - 1| - 7 = -2[/latex]
- [latex]|x + 5| = 0[/latex]
For the following exercises, use the model for the period of a pendulum, [latex]T[/latex], such that [latex]T = 2\pi\sqrt{\dfrac{L}{g}}[/latex], where the length of the pendulum is [latex]L[/latex] and the acceleration due to gravity is [latex]g[/latex].
- If the acceleration due to gravity is [latex]9.8[/latex] m/s[latex]^2[/latex] and the period equals [latex]1[/latex] s, find the length to the nearest cm ([latex]100[/latex] cm = [latex]1[/latex] m).
- If the gravity is [latex]32[/latex] ft/s[latex]^2[/latex] and the period equals [latex]1[/latex] s, find the length to the nearest in. ([latex]12[/latex] in. = [latex]1[/latex] ft). Round your answer to the nearest in.
For the following exercises, use a model for body surface area, BSA, such that [latex]BSA = \sqrt{\dfrac{wh}{3600}}[/latex], where [latex]w[/latex] = weight in kg and [latex]h[/latex] = height in cm.
- Find the height of a [latex]72[/latex]-kg female to the nearest cm whose [latex]BSA = 1.8[/latex].
- Find the weight of a [latex]177[/latex]-cm male to the nearest kg whose [latex]BSA = 2.1[/latex].
For the following exercises, solve the inequality involving absolute value. Write your final answer in interval notation.
- [latex]|x + 9| \geq -6[/latex]
- [latex]|3x - 1| > 11[/latex]
- [latex]|x - 2| + 4 \geq 10[/latex]
- [latex]|x - 7| < -4[/latex]
- [latex]|\dfrac{x-3}{4}| < 2[/latex]