Graphing and Analyzing Linear Equations
For each of the following exercises, find the [latex]x[/latex]-intercept and the [latex]y[/latex]-intercept without graphing. Write the coordinates of each intercept.
- [latex]y = -3x + 6[/latex]
- [latex]3x - 2y = 6[/latex]
- [latex]3x + 8y = 9[/latex]
For each of the following exercises, solve the equation for [latex]y[/latex] in terms of [latex]x[/latex].
- [latex]4x + 2y = 8[/latex]
- [latex]2x = 5 - 3y[/latex]
- [latex]5y + 4 = 10x[/latex]
For each of the following exercises, find the distance between the two points. Simplify your answers, and write the exact answer in simplest radical form for irrational answers.
- [latex](-4, 1) \text{ and } (3, -4)[/latex]
- [latex](5, 0) \text{ and } (5, 6)[/latex]
- Find the distance between the two given points [latex](19, 12) \text{ and } (41, 71)[/latex] using your calculator, and round your answer to the nearest hundredth.
For each of the following exercises, find the coordinates of the midpoint of the line segment that joins the two given points.
- [latex](-1, 1) \text{ and } (7, -4)[/latex]
- [latex](0, 7) \text{ and } (4, -9)[/latex]
For each of the following exercises, identify the information requested.
- What are the coordinates of the origin?
- If a point is located on the y-axis, what is the x-coordinate?
- If a point is located on the x-axis, what is the y-coordinate?
For each of the following exercises, plot the three points on the given coordinate plane. State whether the three points you plotted appear to be collinear (on the same line).
- [latex](-1, 2), (0, 4), (2, 1)[/latex]
Empty coordinate plane - Name the coordinates of the points graphed.
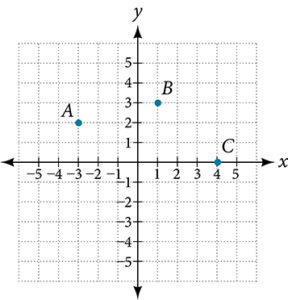
Coordinate plane with points A,B,C
For each of the following exercises, construct a table and graph the equation by plotting at least three points.
- [latex]y = \frac{1}{3}x + 2[/latex]
- [latex]2y = x + 3[/latex]
For each of the following exercises, find and plot the [latex]x[/latex]– and [latex]y[/latex]-intercepts, and graph the straight line based on those two points.
- [latex]x - 2y = 8[/latex]
- [latex]3y = -2x + 6[/latex]
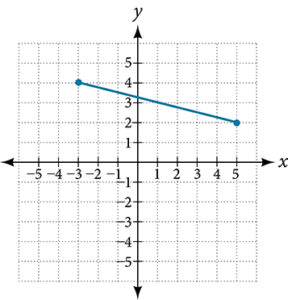
For each of the following exercises, use the graph in the figure below.
- Find the distance between the two endpoints using the distance formula. Round to three decimal places.
- Find the coordinates of the midpoint of the line segment connecting the two points.
- Find the distance that [latex](-3, 4)[/latex] is from the origin.
- Find the distance that [latex](5, 2)[/latex] is from the origin. Round to three decimal places.
- Which point is closer to the origin?
For the following exercises, find the slope of the line that passes through the given points.
- [latex](5, 4)[/latex] and [latex](7, 9)[/latex]
- [latex](-3, 2)[/latex] and [latex](4, -7)[/latex]
- [latex](-5, 4)[/latex] and [latex](2, 4)[/latex]
- [latex](-1, -2)[/latex] and [latex](3, 4)[/latex]
- [latex](3, -2)[/latex] and [latex](3, -2)[/latex]
Equations of Lines
For the following exercises, solve the equation for [latex]x[/latex].
- [latex]4x - 3 = 5[/latex]
- [latex]12 - 5(x + 3) = 2x - 5[/latex]
- [latex]\dfrac{x}{3} - \dfrac{3}{4} = \dfrac{2x + 3}{12}[/latex]
- [latex]3(2x - 1) + x = 5x + 3[/latex]
- [latex]\dfrac{x+2}{4} - \dfrac{x-1}{3} = 2[/latex]
For the following exercises, solve each rational equation for [latex]x[/latex]. State all [latex]x[/latex]-values that are excluded from the solution set.
- [latex]2 - \dfrac{3}{x + 4} = \dfrac{x + 2}{x + 4}[/latex]
- [latex]\dfrac{3x}{x - 1} + 2 = \dfrac{3}{x - 1}[/latex]
- [latex]\dfrac{1}{x} = \dfrac{1}{5} + \dfrac{3}{2x}[/latex]
For the following exercises, find the equation of the line using the point-slope formula. Write all the final equations using the slope-intercept form.
- [latex](1, 2)[/latex] with a slope of [latex]-\dfrac{4}{5}[/latex]
- [latex]y[/latex]-intercept is [latex]2[/latex], and [latex](4, -1)[/latex]
- [latex](1, 3)[/latex] and [latex](5, 5)[/latex]
- perpendicular to [latex]3y = x - 4[/latex] and passes through the point [latex](-2, 1)[/latex]
For the following exercises, find the equation of the line using the given information.
- [latex](1, 7)[/latex] and [latex](3, 7)[/latex]
- The slope equals zero and it passes through the point [latex](1, -4)[/latex]
- [latex](-1, 3)[/latex] and [latex](4, -5)[/latex]
For the following exercises, graph the pair of equations on the same axes, and state whether they are parallel, perpendicular, or neither.
- [latex]3x - 2y = 5[/latex] and [latex]6y - 9x = 6[/latex]
- [latex]x = 4[/latex] and [latex]y = -3[/latex]
Modeling with Linear Equations
- If the total amount of money you had to invest was [latex]$2,000[/latex] and you deposit [latex]x[/latex] amount in one investment, how can you represent the remaining amount?
- If Bill was traveling [latex]v[/latex] mi/h, how would you represent Daemon’s speed if he was traveling [latex]10[/latex] mi/h faster?
For the following exercise, use the information to find a linear algebraic equation model to use to answer the question being asked.
- Beth and Ann are joking that their combined ages equal Sam’s age. If Beth is twice Ann’s age and Sam is [latex]69[/latex] yr old, what are Beth and Ann’s ages?
For the following exercises, use this scenario: Two different telephone carriers offer the following plans that a person is considering. Company A has a monthly fee of [latex]$20[/latex] and charges of [latex]$0.05[/latex]/min for calls. Company B has a monthly fee of [latex]$5[/latex] and charges [latex]$0.10[/latex]/min for calls.
- Find the model of the total cost of Company A’s plan, using [latex]m[/latex] for the minutes.
- Find the model of the total cost of Company B’s plan, using [latex]m[/latex] for the minutes.
- Find out how many minutes of calling would make the two plans equal.
- If the person makes a monthly average of [latex]200[/latex] min of calls, which plan should for the person choose?
For the following exercises, use this scenario: A wireless carrier offers the following plans that a person is considering. The Family Plan: [latex]$90[/latex] monthly fee, unlimited talk and text on up to [latex]8[/latex] lines, and data charges of [latex]$40[/latex] for each device for up to [latex]2[/latex] GB of data per device. The Mobile Share Plan: [latex]$120[/latex] monthly fee for up to [latex]10[/latex] devices, unlimited talk and text for all the lines, and data charges of [latex]$35[/latex] for each device up to a shared [latex]total of [latex]10[/latex] GB of data. Use [latex]P[/latex] for the number of devices that need data plans as part of their cost.
- Find the model of the total cost of the Family Plan.
- Find the model of the total cost of the Mobile Share Plan.
- Assuming they stay under their data limit, find the number of devices that would make the two plans equal in cost.
- If a family has [latex]3[/latex] smart phones, which plan should they choose?
For exercises 12 and 13, use this scenario: A retired woman has [latex]50,000[/latex] to invest but needs to make [latex]6,000[/latex] a year from the interest to meet certain living expenses. One bond investment pays [latex]15\%[/latex] annual interest. The rest of it she wants to put in a CD that pays [latex]7\%[/latex].
- If we let [latex]x[/latex] be the amount the woman invests in the [latex]15\%[/latex] bond, how much will she be able to invest in the CD?
- Set up and solve the equation for how much the woman should invest in each option to sustain a [latex]6,000[/latex] annual return.
- Two planes fly in opposite directions. One travels [latex]450 \, \text{mi/h}[/latex] and the other [latex]550 \, \text{mi/h}[/latex]. How long will it take before they are [latex]4{,}000 \, \text{mi}[/latex] apart?
- Fiora starts riding her bike at [latex]20 \, \text{mi/h}[/latex]. After a while, she slows down to [latex]12 \, \text{mi/h}[/latex], and maintains that speed for the rest of the trip. The whole trip of [latex]70 \, \text{mi}[/latex] takes her [latex]4.5 \, \text{h}[/latex]. For what distance did she travel at [latex]20 \, \text{mi/h}[/latex]?
- Raúl has [latex]\$20{,}000[/latex] to invest. His intent is to earn [latex]11\%[/latex] interest on his investment. He can invest part of his money at [latex]8\%[/latex] interest and part at [latex]12\%[/latex] interest. How much does Raúl need to invest in each option to make a total [latex]11\%[/latex] return on his [latex]\$20{,}000[/latex]?
For the following exercises, use this scenario: A truck rental agency offers two kinds of plans. Plan A charges [latex]$75/\text{wk}[/latex] plus [latex]$0.10/\text{mi}[/latex] driven. Plan B charges [latex]$100/\text{wk}[/latex] plus [latex]$0.05/\text{mi}[/latex] driven.
- Write the model equation for the cost of renting a truck with plan A.
- Write the model equation for the cost of renting a truck with plan B.
- Find the number of miles that would generate the same cost for both plans.
- If Tim knows he has to travel [latex]300 \, \text{mi}[/latex], which plan should he choose?
For the following exercises, use the formula given to solve for the required value.
- The formula [latex]F = \dfrac{mv^2}{R}[/latex] relates force ([latex]F[/latex]), velocity ([latex]v[/latex]), mass ([latex]m[/latex]), and resistance ([latex]R[/latex]). Find [latex]R[/latex] when [latex]m = 45[/latex], [latex]v = 7[/latex], and [latex]F = 245[/latex].
- [latex]\text{Sum} = \dfrac{1}{1 - r}[/latex] is the formula for an infinite series sum. If the sum is [latex]5[/latex], find [latex]r[/latex].
For the following exercises, solve for the given variable in the formula. After obtaining a new version of the formula, you will use it to solve a question.
- Solve for [latex]W[/latex]: [latex]P = 2L + 2W[/latex]
- Use the formula from the previous question to find the width, [latex]W[/latex], of a rectangle whose length is [latex]15[/latex] and whose perimeter is [latex]58[/latex].
- Solve for [latex]f[/latex]: [latex]\dfrac{1}{p} + \dfrac{1}{q} = \dfrac{1}{f}[/latex]
- Use the formula from the previous question to find [latex]f[/latex] when [latex]p = 8[/latex] and [latex]q = 13[/latex].
- Solve for [latex]m[/latex] in the slope-intercept formula: [latex]y = mx + b[/latex]
- Use the formula from the previous question to find [latex]m[/latex] when the coordinates of the point are ([latex]4[/latex], [latex]7[/latex]) and [latex]b = 12[/latex].
- The area of a trapezoid is given by [latex]A = \dfrac{1}{2} h (b_1 + b_2)[/latex]. Use the formula to find the area of a trapezoid with [latex]h = 6[/latex], [latex]b_1 = 14[/latex], and [latex]b_2 = 8[/latex].
- Solve for [latex]h[/latex]: [latex]A = \dfrac{1}{2} h (b_1 + b_2)[/latex]
- Use the formula from the previous question to find the height of a trapezoid with [latex]A = 150[/latex], [latex]b_1 = 19[/latex], and [latex]b_2 = 11[/latex].
- Find the dimensions of an American football field. The length is [latex]200 \, \text{ft}[/latex] more than the width, and the perimeter is [latex]1{,}040 \, \text{ft}[/latex]. Find the length and width. Use the perimeter formula [latex]P = 2L + 2W[/latex].
- Distance equals rate times time, [latex]d = rt[/latex]. Find the distance Tom travels if he is moving at a rate of [latex]55 \, \text{mi/h}[/latex] for [latex]3.5 \, \text{h}[/latex].
- Using the formula in the previous exercise, find the distance that Susan travels if she is moving at a rate of [latex]60 \, \text{mi/h}[/latex] for [latex]6.75 \, \text{h}[/latex].
- Solve for [latex]h[/latex]: [latex]A = \dfrac{1}{2} b h[/latex]
- Use the formula from the previous question to find the height to the nearest tenth of a triangle with a base of [latex]15[/latex] and an area of [latex]215[/latex].
- The volume formula for a cylinder is [latex]V = \pi r^2 h[/latex]. Using the symbol [latex]\pi[/latex] in your answer, find the volume of a cylinder with a radius, [latex]r[/latex], of [latex]4 \, \text{cm}[/latex] and a height of [latex]14 \, \text{cm}[/latex].
- Solve for [latex]h[/latex]: [latex]V = \pi r^2 h[/latex]
- Use the formula from the previous question to find the height of a cylinder with a radius of [latex]8[/latex] and a volume of [latex]16\pi[/latex].
- Solve for [latex]r[/latex]: [latex]V = \pi r^2 h[/latex]
- Use the formula from the previous question to find the radius of a cylinder with a height of [latex]36[/latex] and a volume of [latex]324\pi[/latex].
- The formula for the circumference of a circle is [latex]C = 2 \pi r[/latex]. Find the circumference of a circle with a diameter of [latex]12 \, \text{in.}[/latex] (diameter = [latex]2r[/latex]). Use the symbol [latex]\pi[/latex] in your final answer.
- Solve the formula from the previous question for [latex]\pi[/latex]. Notice why [latex]\pi[/latex] is sometimes defined as the ratio of the circumference to its diameter.
Linear Inequalities
For the following exercises, solve the inequality. Write your final answer in interval notation.
- [latex]3x + 2 \geq 7x - 1[/latex]
- [latex]4(x + 3) \geq 2x - 1[/latex]
- [latex]-5(x - 1) + 3 > 3x - 4 - 4x[/latex]
- [latex]\dfrac{x + 3}{8} - \dfrac{x + 5}{5} \geq \dfrac{3}{10}[/latex]
For the following exercises, solve the compound inequality. Express your answer using inequality signs, and then write your answer using interval notation.
- [latex]-4 < 3x + 2 \leq 18[/latex]
- [latex]3x + 1 > 2x - 5 > x - 7[/latex]
- [latex]3y < 5 - 2y < 7 + y[/latex]
- [latex]2x - 5 \leq -11 \, \text{or} \, 5x + 1 \geq 6[/latex]
- [latex]x + 7 < x + 2[/latex]
For the following exercises, write the set in interval notation.
- [latex]\{ x \, | \, -1 < x < 3 \}[/latex]
- [latex]\{ x \, | \, x < 4 \}[/latex]
For the following exercises, write the interval in set-builder notation.
- [latex](-\infty, 6)[/latex]
- [latex][-3, 5)[/latex]
For the following exercises, write the set of numbers represented on the number line in interval notation.
-

Number line with open circle at -2 and closed circle at -1 -

Number line with closed circle at 4 and left-facing arrow