Parallel and Perpendicular Lines
Parallel lines are a key idea in geometry. They are lines that stay the same distance apart over their entire length and never cross each other, no matter how long they extend. This consistent distance between them is called equidistance. In simpler terms, no matter how far you extend parallel lines, they will always run alongside each other and never meet. This makes them an important concept to understand, especially when studying shapes, angles, and various design and engineering principles.
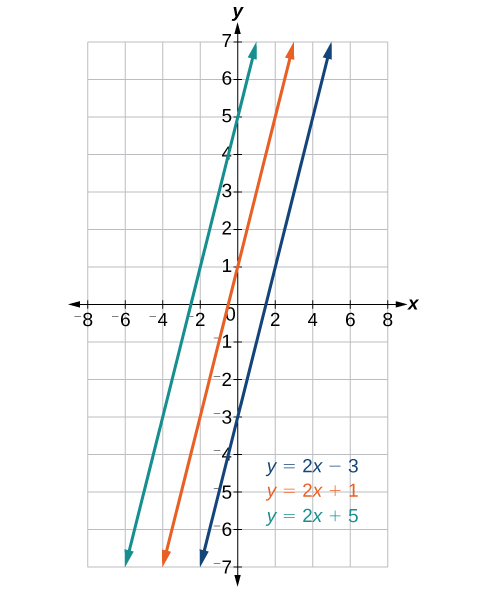
All of the lines shown in the graph are parallel because they have the same slope and different y-intercepts.
parallel lines
Parallel lines are defined as lines in a plane that do not intersect because they have the same slope, maintaining a consistent direction and steepness.
Lines that are perpendicular intersect to form a [latex]{90}^{\circ }[/latex] angle. The slope of one line is the negative reciprocal of the other. We can show that two lines are perpendicular if the product of the two slopes is [latex]-1:{m}_{1}\cdot {m}_{2}=-1[/latex].
[latex]\begin{array}{l}\text{ }{m}_{1}\cdot {m}_{2}=-1\hfill \\ \text{ }3\cdot \left(-\dfrac{1}{3}\right)=-1\hfill \end{array}[/latex]
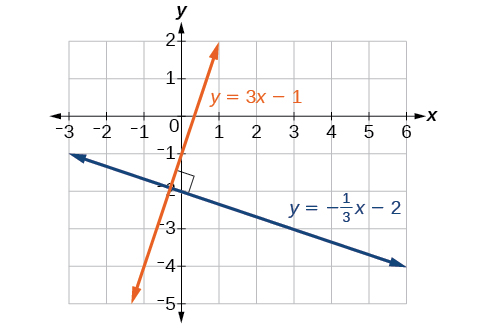
perpendicular lines
Lines that are perpendicular intersect to form a [latex]{90}^{\circ }[/latex] angle.
This relationship occurs when the slopes of two lines are negative reciprocals of each other, meaning if one line has a slope of [latex]m[/latex], the perpendicular line will have a slope of [latex]-\dfrac{1}{m}[/latex].
