Series and Summation Notation

Now that we’ve explored sequences, let’s take it a step further and talk about series. While a sequence lists numbers in a specific order, a series is what you get when you add those numbers together. In other words, a series is the sum of the terms in a sequence. Understanding how to work with series is important because it allows us to find the total of a sequence of numbers, which has many practical applications in mathematics and beyond.

Summation notation is used to represent series. Summation notation is often known as sigma notation because it uses the Greek capital letter sigma, [latex]\Sigma[/latex], to represent the sum. Summation notation includes an explicit formula and specifies the first and last terms in the series. An explicit formula for each term of the series is given to the right of the sigma. A variable called the index of summation is written below the sigma. The index of summation is set equal to the lower limit of summation, which is the number used to generate the first term in the series. The number above the sigma, called the upper limit of summation, is the number used to generate the last term in a series.

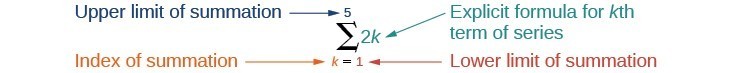
If we interpret the given notation, we see that it asks us to find the sum of the terms in the series [latex]{a}_{k}=2k[/latex] for [latex]k=1[/latex] through [latex]k=5[/latex]. We can begin by substituting the terms for [latex]k[/latex] and listing out the terms of this series.

[latex]\begin{align} &{a}_{1}=2\left(1\right)=2 \\ &{a}_{2}=2\left(2\right)=4 \\ &{a}_{3}=2\left(3\right)=6 \\ &{a}_{4}=2\left(4\right)=8 \\ &{a}_{5}=2\left(5\right)=10 \end{align}[/latex]

We can find the sum of the series by adding the terms:

[latex]\sum\limits _{k=1}^{5}2k=2+4+6+8+10=30[/latex]