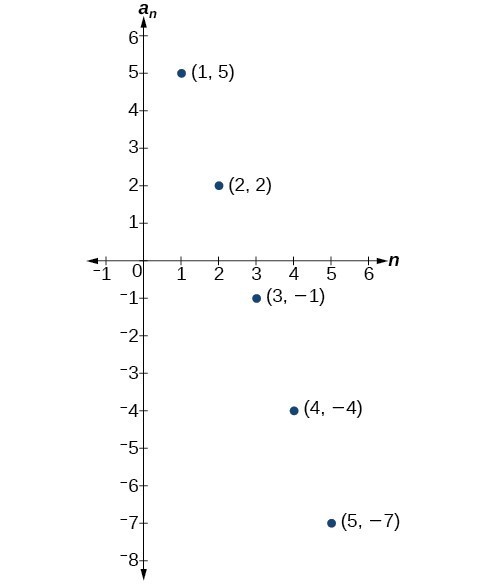- Write the terms of a sequence defined by an explicit formula and a recursive formula
- Use factorial notation
Sequences Defined by an Explicit Formula
A video game company launches an exciting new advertising campaign. They predict the number of online visits to their website, or hits, will double each day. The model they are using shows [latex]2[/latex] hits the first day, [latex]4[/latex] hits the second day, [latex]8[/latex] hits the third day, and so on.
| Day | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | … |
| Hits | [latex]2[/latex] | [latex]4[/latex] | [latex]8[/latex] | [latex]16[/latex] | [latex]32[/latex] | … |
If their model continues, how many hits will there be at the end of the month? To answer this question, we’ll first need to know how to determine a list of numbers written in a specific order. One way to describe an ordered list of numbers is as a sequence. A sequence is a function whose domain is a subset of the counting numbers. The sequence established by the number of hits on the website is
[latex]\left\{2,4,8,16,32,\dots \right\}[/latex].
The ellipsis (…) indicates that the sequence continues indefinitely. Each number in the sequence is called a term. The first five terms of this sequence are [latex]2[/latex], [latex]4[/latex], [latex]8[/latex], [latex]16[/latex], and [latex]32[/latex].
Listing all of the terms for a sequence can be cumbersome. For example, finding the number of hits on the website at the end of the month would require listing out as many as [latex]31[/latex] terms. A more efficient way to determine a specific term is by writing a formula to define the sequence.
One type of formula is an explicit formula, which defines the terms of a sequence using their position in the sequence. Explicit formulas are helpful if we want to find a specific term of a sequence without finding all of the previous terms. We can use the formula to find the [latex]n\text{th}[/latex] term of the sequence, where [latex]n[/latex] is any positive number. In our example, each number in the sequence is double the previous number, so we can use powers of [latex]2[/latex] to write a formula for the [latex]n\text{th}[/latex] term.

The first term of the sequence is [latex]{2}^{1}=2[/latex], the second term is [latex]{2}^{2}=4[/latex], the third term is [latex]{2}^{3}=8[/latex], and so on. The [latex]n\text{th}[/latex] term of the sequence can be found by raising 2 to the [latex]n\text{th}[/latex] power. An explicit formula for a sequence is named by a lower case letter [latex]a,b,c..[/latex]. with the subscript [latex]n[/latex]. The explicit formula for this sequence is
[latex]{a}_{n}={2}^{n}[/latex].
Another way to represent the sequence is by using a table. The first five terms of the sequence and the [latex]n\text{th}[/latex] term of the sequence are shown in the table.
| [latex]n[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]n[/latex] |
| [latex]n\text{th}[/latex] term of the sequence, [latex]{a}_{n}[/latex] | [latex]2[/latex] | [latex]4[/latex] | [latex]8[/latex] | [latex]16[/latex] | [latex]32[/latex] | [latex]{2}^{n}[/latex] |
Graphing provides a visual representation of the sequence as a set of distinct points. We can see from the graph below that the number of hits is rising at an exponential rate. This particular sequence forms an exponential function.
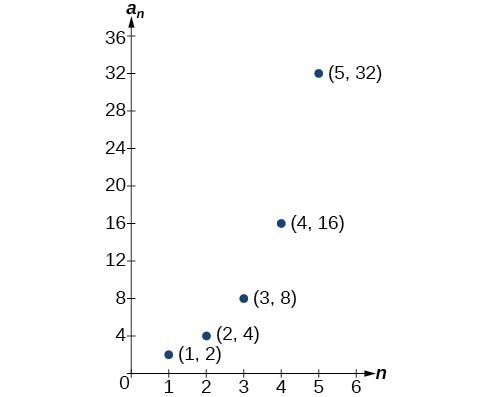
Lastly, we can write this particular sequence as
[latex]\left\{2,4,8,16,32,\dots ,{2}^{n},\dots \right\}[/latex].
A sequence that continues indefinitely is called an infinite sequence. The domain of an infinite sequence is the set of counting numbers. If we consider only the first [latex]10[/latex] terms of the sequence, we could write
[latex]\left\{2,4,8,16,32,\dots ,1024\right\}[/latex]
This sequence is called a finite sequence because it does not continue indefinitely.
sequence
A sequence is a function whose domain is the set of positive integers. Each number in the sequence is called a term, and there’s a rule or pattern that tells you how to find each term.
- A finite sequence is a sequence whose domain consists of only the first [latex]n[/latex] positive integers. The variable [latex]a[/latex] with a number subscript is used to represent the terms in a sequence and to indicate the position of the term in the sequence.
[latex]{a}_{1},{a}_{2},{a}_{3},\dots ,{a}_{n},\dots[/latex]
We call [latex]{a}_{1}[/latex] the first term of the sequence, [latex]{a}_{2}[/latex] the second term of the sequence, [latex]{a}_{3}[/latex] the third term of the sequence, and so on. The term [latex]{a}_{n}[/latex] is called the [latex]n\text{th}[/latex] term of the sequence, or the general term of the sequence. An explicit formula defines the [latex]n\text{th}[/latex] term of a sequence using the position of the term.
- A sequence that continues indefinitely is an infinite sequence. The ellipsis [latex](...)[/latex] is used to indicate that the sequence continues indefinitely.
Sequences can be simple, like adding a constant to get the next number, or they can be more complex, with different rules that might involve multiplication, division, or other operations.
- Substitute each value of [latex]n[/latex] into the formula. Begin with [latex]n=1[/latex] to find the first term, [latex]{a}_{1}[/latex].
- To find the second term, [latex]{a}_{2}[/latex], use [latex]n=2[/latex].
- Continue in the same manner until you have identified all [latex]n[/latex] terms.
Investigating Explicit Formulas
We’ve learned that sequences are functions whose domain is over the positive integers. This is true for other types of functions, including some piecewise functions. Recall that a piecewise function is a function defined by multiple subsections. A different formula might represent each individual subsection.
- Identify the formula to which [latex]n=1[/latex] applies.
- To find the first term, [latex]{a}_{1}[/latex], use [latex]n=1[/latex] in the appropriate formula.
- Identify the formula to which [latex]n=2[/latex] applies.
- To find the second term, [latex]{a}_{2}[/latex], use [latex]n=2[/latex] in the appropriate formula.
- Continue in the same manner until you have identified all [latex]n[/latex] terms.
[latex]{a_{n}}=\begin{cases}n^{2} & \text{if }n\text{ is not divisible by 3} \\[1mm] \dfrac{n}{3} & \text{if }n\text{ is divisible by 3}\end{cases}[/latex]