- Draw parabolas on a graph, understanding how their shapes change based on whether their vertex is at the origin or another point
- Write equations of parabolas in standard form
- Solve applied problems involving parabolas
Parabolas
To work with parabolas in the coordinate plane, we consider two cases: those with a vertex at the origin and those with a vertex at a point other than the origin. We begin with the former.
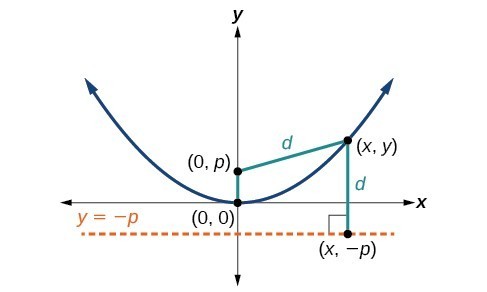
Let [latex]\left(x,y\right)[/latex] be a point on the parabola with vertex [latex]\left(0,0\right)[/latex], focus [latex]\left(0,p\right)[/latex], and directrix [latex]y= -p[/latex] as shown in Figure 4. The distance [latex]d[/latex] from point [latex]\left(x,y\right)[/latex] to point [latex]\left(x,-p\right)[/latex] on the directrix is the difference of the y-values: [latex]d=y+p[/latex]. The distance from the focus [latex]\left(0,p\right)[/latex] to the point [latex]\left(x,y\right)[/latex] is also equal to [latex]d[/latex] and can be expressed using the distance formula.
[latex]\begin{align}d&=\sqrt{{\left(x - 0\right)}^{2}+{\left(y-p\right)}^{2}} \\ &=\sqrt{{x}^{2}+{\left(y-p\right)}^{2}} \end{align}[/latex]
Set the two expressions for [latex]d[/latex] equal to each other and solve for [latex]y[/latex] to derive the equation of the parabola. We do this because the distance from [latex]\left(x,y\right)[/latex] to [latex]\left(0,p\right)[/latex] equals the distance from [latex]\left(x,y\right)[/latex] to [latex]\left(x, -p\right)[/latex].
[latex]\sqrt{{x}^{2}+{\left(y-p\right)}^{2}}=y+p[/latex]
We then square both sides of the equation, expand the squared terms, and simplify by combining like terms.
[latex]\begin{gathered}{x}^{2}+{\left(y-p\right)}^{2}={\left(y+p\right)}^{2} \\ {x}^{2}+{y}^{2}-2py+{p}^{2}={y}^{2}+2py+{p}^{2}\\ {x}^{2}-2py=2py \\ {x}^{2}=4py\end{gathered}[/latex]
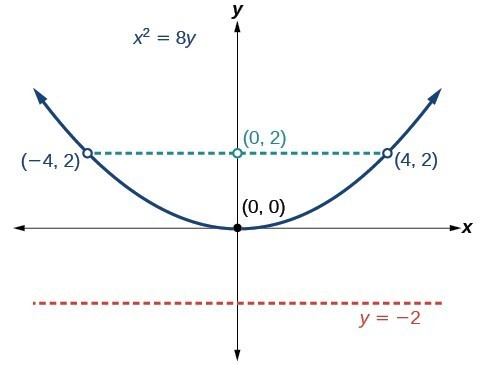
The equations of parabolas with vertex [latex]\left(0,0\right)[/latex] are [latex]{y}^{2}=4px[/latex] when the x-axis is the axis of symmetry and [latex]{x}^{2}=4py[/latex] when the y-axis is the axis of symmetry.
Graphing Parabolas with Vertices at the Origin
The Main Idea
- Standard Forms:
- Vertical parabolas: [latex]x^2 = 4py[/latex]
- Horizontal parabolas: [latex]y^2 = 4px[/latex]
- Key Features:
- Vertex: Always at [latex](0, 0)[/latex] for these standard forms
- Axis of symmetry: [latex]x[/latex]-axis for horizontal parabolas, [latex]y[/latex]-axis for vertical parabolas
- Focus: [latex](p, 0)[/latex] for horizontal parabolas, [latex](0, p)[/latex] for vertical parabolas
- Directrix: [latex]x = -p[/latex] for horizontal parabolas, [latex]y = -p[/latex] for vertical parabolas
- Focal diameter endpoints: [latex](p, ±2p)[/latex] for horizontal parabolas, [latex](±2p, p)[/latex] for vertical parabolas
- Direction of Opening:
- Horizontal parabolas: Right if [latex]p > 0[/latex], Left if [latex]p < 0[/latex]
- Vertical parabolas: Up if [latex]p > 0[/latex], Down if [latex]p < 0[/latex]
- Tangent Lines:
- Tangent lines at the endpoints of the focal diameter intersect on the axis of symmetry
You can view the transcript for “Conic Sections: The Parabola part 1 of 2” here (opens in new window).
You can view the transcript for “Conic Sections: The Parabola part 2 of 2” here (opens in new window).
Writing Equations of Parabolas in Standard Form
The Main Idea
- Standard Forms:
- Horizontal parabolas: [latex]y^2 = 4px[/latex] (focus form: [latex](p, 0)[/latex])
- Vertical parabolas: [latex]x^2 = 4py[/latex] (focus form: [latex](0, p)[/latex])
- Key Features Used:
- Focus coordinates
- Directrix equation
- Process:
- Identify axis of symmetry based on focus coordinates
- Calculate [latex]4p[/latex] using focus coordinates
- Substitute [latex]4p[/latex] into the appropriate standard form equation
- Distinction:
- These are equations of parabolas as geometric objects, not quadratic functions
- Specific language is used to describe these geometric forms
You can view the transcript for “Ex 2: Conic Section: Parabola with Vertical Axis and Vertex at the Origin (Down)” here (opens in new window).
You can view the transcript for “Ex 3: Conic Section: Parabola with Horizontal Axis and Vertex at the Origin (Right)” here (opens in new window).
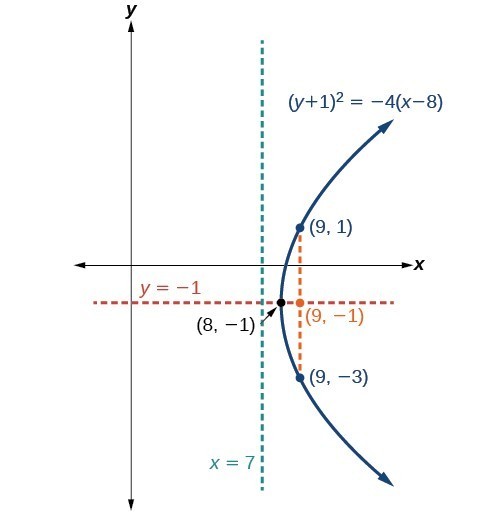
Parabolas with Vertices Not at the Origin
The Main Idea
- Translated Standard Forms:
- Horizontal parabolas: [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex]
- Vertical parabolas: [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex]
- Key Features:
- Vertex: [latex](h, k)[/latex]
- Axis of symmetry: [latex]x = h[/latex] (vertical) or [latex]y = k[/latex] (horizontal)
- Focus: [latex](h+p, k)[/latex] for horizontal, [latex](h, k+p)[/latex] for vertical
- Directrix: [latex]x = h-p[/latex] for horizontal, [latex]y = k-p[/latex] for vertical
- Opening Direction:
- Horizontal: Right if [latex]p > 0[/latex], Left if [latex]p < 0[/latex]
- Vertical: Up if [latex]p > 0[/latex], Down if [latex]p < 0[/latex]
- Completing the Square:
- Used to convert non-standard equations into standard form