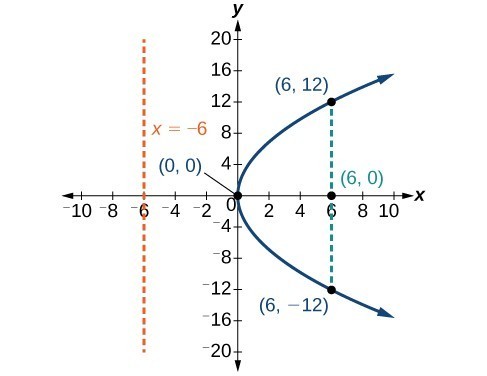
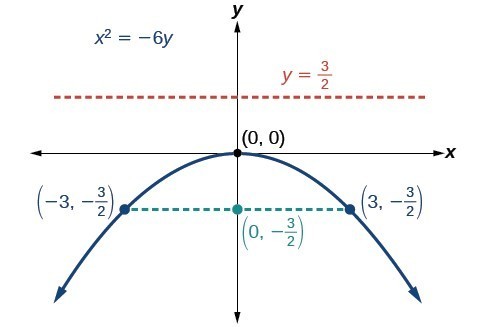
Graphing Parabolas with Vertices at the Origin
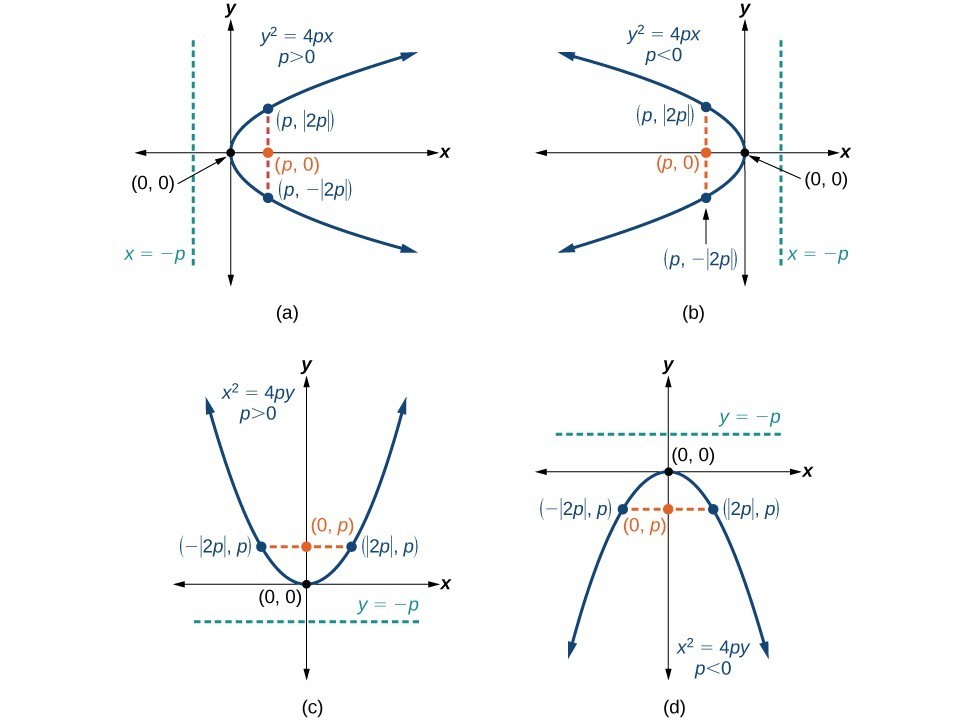
standard forms of parabolas with vertex [latex](0, 0)[/latex]
The table below summarizes the standard features of parabolas with a vertex at the origin.
| Axis of Symmetry | Equation | Focus | Directrix | Endpoints of Focal Diameter |
| [latex]x[/latex]-axis | [latex]{y}^{2}=4px[/latex] | [latex]\left(p,\text{ }0\right)[/latex] | [latex]x=-p[/latex] | [latex]\left(p,\text{ }\pm 2p\right)[/latex] |
| [latex]y[/latex]-axis | [latex]{x}^{2}=4py[/latex] | [latex]\left(0,\text{ }p\right)[/latex] | [latex]y=-p[/latex] | [latex]\left(\pm 2p,\text{ }p\right)[/latex] |
The key features of a parabola are its vertex, axis of symmetry, focus, directrix, and focal diameter. When given a standard equation for a parabola centered at the origin, we can easily identify the key features to graph the parabola.
A line is said to be tangent to a curve if it intersects the curve at exactly one point. If we sketch lines tangent to the parabola at the endpoints of the focal diameter, these lines intersect on the axis of symmetry.
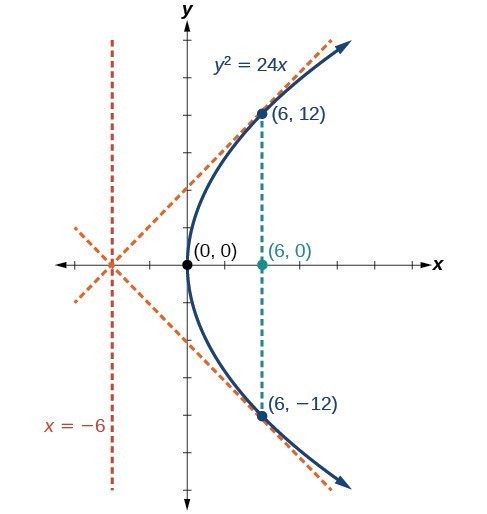
- Determine which of the standard forms applies to the given equation: [latex]{y}^{2}=4px[/latex] or [latex]{x}^{2}=4py[/latex].
- Use the standard form identified in Step 1 to determine the axis of symmetry, focus, equation of the directrix, and endpoints of the focal diameter.
- If the equation is in the form [latex]{y}^{2}=4px[/latex], then
- the axis of symmetry is the [latex]x[/latex]-axis, [latex]y=0[/latex]
- set [latex]4p[/latex] equal to the coefficient of [latex]x[/latex] in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens right. If [latex]p<0[/latex], the parabola opens left.
- use [latex]p[/latex] to find the coordinates of the focus, [latex]\left(p,0\right)[/latex]
- use [latex]p[/latex] to find the equation of the directrix, [latex]x=-p[/latex]
- use [latex]p[/latex] to find the endpoints of the focal diameter, [latex]\left(p,\pm 2p\right)[/latex]. Alternately, substitute [latex]x=p[/latex] into the original equation.
- If the equation is in the form [latex]{x}^{2}=4py[/latex], then
- the axis of symmetry is the [latex]y[/latex]-axis, [latex]x=0[/latex]
- set [latex]4p[/latex] equal to the coefficient of [latex]y[/latex] in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens up. If [latex]p<0[/latex], the parabola opens down.
- use [latex]p[/latex] to find the coordinates of the focus, [latex]\left(0,p\right)[/latex]
- use [latex]p[/latex] to find equation of the directrix, [latex]y=-p[/latex]
- use [latex]p[/latex] to find the endpoints of the focal diameter, [latex]\left(\pm 2p,p\right)[/latex]
- If the equation is in the form [latex]{y}^{2}=4px[/latex], then
- Plot the focus, directrix, and focal diameter, and draw a smooth curve to form the parabola.