- Draw parabolas on a graph, understanding how their shapes change based on whether their vertex is at the origin or another point
- Write equations of parabolas in standard form
- Solve applied problems involving parabolas

Katherine Johnson is the pioneering NASA mathematician who was integral to the successful and safe flight and return of many human missions as well as satellites. Prior to the work featured in the movie Hidden Figures, she had already made major contributions to the space program. She provided trajectory analysis for the Mercury mission, in which Alan Shepard became the first American to reach space, and she and engineer Ted Sopinski authored a monumental paper regarding placing an object in a precise orbital position and having it return safely to Earth. Many of the orbits she determined were made up of parabolas, and her ability to combine different types of math enabled an unprecedented level of precision. Johnson said, “You tell me when you want it and where you want it to land, and I’ll do it backwards and tell you when to take off.”
Johnson’s work on parabolic orbits and other complex mathematics resulted in successful orbits, Moon landings, and the development of the Space Shuttle program. Applications of parabolas are also critical to other areas of science. Parabolic mirrors (or reflectors) are able to capture energy and focus it to a single point. The advantages of this property are evidenced by the vast list of parabolic objects we use every day: satellite dishes, suspension bridges, telescopes, microphones, spotlights, and car headlights, to name a few. Parabolic reflectors are also used in alternative energy devices, such as solar cookers and water heaters, because they are inexpensive to manufacture and need little maintenance. In this section we will explore the parabola and its uses, including low-cost, energy-efficient solar designs.
Parabolas
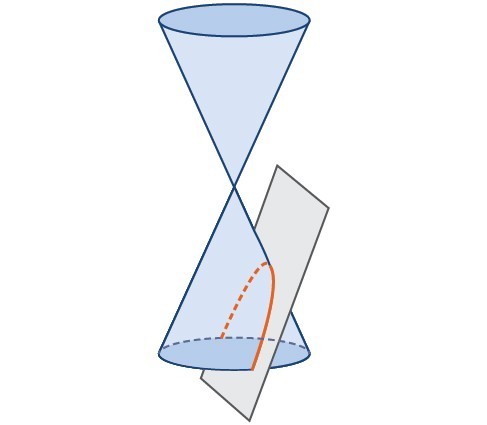
A parabola is a U-shaped curve that is the result of intersecting a cone with a plane parallel to one of the cone’s sides. This unique intersection creates a symmetrical open curve.
Like the ellipse and hyperbola, the parabola can also be defined by a set of points in the coordinate plane. A parabola is the set of all points [latex]\left(x,y\right)[/latex] in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix. Other key features of a parabola are its vertex, axis of symmetry, and focal diameter.
parabola
A parabola is all points in a plane that are the same distance from a fixed point and a fixed line.
-
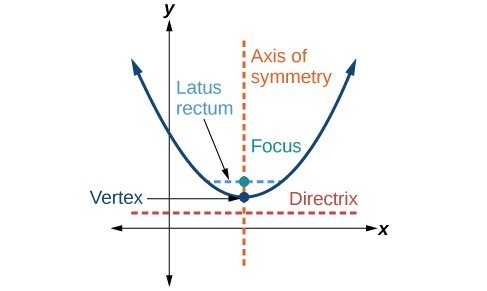
Key features of a parabola The fixed point is called the focus.
- The fixed line is called the directrix of the parabola.
- The axis of symmetry passes through the focus and vertex and is perpendicular to the directrix.
- The vertex is the midpoint between the directrix and the focus.
- The line segment that passes through the focus and is parallel to the directrix is called the latus rectum.The endpoints of the latus rectum lie on the curve.