Hyperbola: Learn It 3

Hyperbolas Not Centered at the Origin

Like the graphs for other equations, the graph of a hyperbola can be translated. If a hyperbola is translated units horizontally and units vertically, the center of the hyperbola will be [latex](h,k)[/latex]. This translation results in the standard form of the equation we saw previously, with [latex]x[/latex] replaced by [latex](x-h)[/latex] and [latex]y[/latex] replaced by [latex](y-k)[/latex].

standard forms of the equation of a hyperbola with center [latex](h,k)[/latex]

The standard form of the equation of a hyperbola with center [latex]\left(h,k\right)[/latex] and transverse axis parallel to the [latex]x[/latex]-axis is

[latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}-\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex]

where

  • the length of the transverse axis is [latex]2a[/latex]
  • the coordinates of the vertices are [latex]\left(h\pm a,k\right)[/latex]
  • the length of the conjugate axis is [latex]2b[/latex]
  • the coordinates of the co-vertices are [latex]\left(h,k\pm b\right)[/latex]
  • the distance between the foci is [latex]2c[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]
  • the coordinates of the foci are [latex]\left(h\pm c,k\right)[/latex]
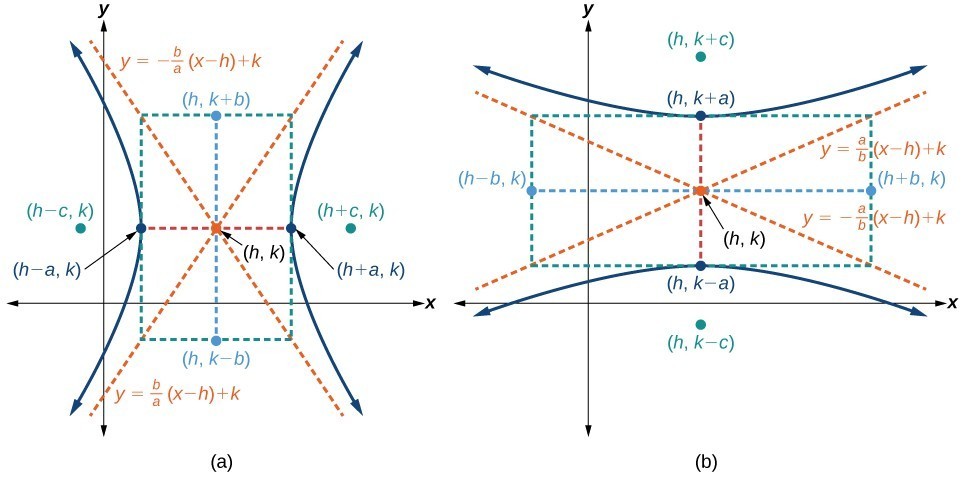
(a) Horizontal hyperbola with center [latex]\left(h,k\right)[/latex] (b) Vertical hyperbola with center [latex]\left(h,k\right)[/latex]

Like hyperbolas centered at the origin, hyperbolas centered at a point [latex]\left(h,k\right)[/latex] have vertices, co-vertices, and foci that are related by the equation [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]. We can use this relationship along with the midpoint and distance formulas to find the standard equation of a hyperbola when the vertices and foci are given.

How To: Given the vertices and foci of a hyperbola centered at [latex]\left(h,k\right)[/latex], write its equation in standard form.

  1. Determine whether the transverse axis is parallel to the [latex]x[/latex]– or [latex]y[/latex]-axis.
    1. If the [latex]y[/latex]-coordinates of the given vertices and foci are the same, then the transverse axis is parallel to the [latex]x[/latex]-axis. Use the standard form [latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}-\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex].
    2. If the [latex]x[/latex]-coordinates of the given vertices and foci are the same, then the transverse axis is parallel to the [latex]y[/latex]-axis. Use the standard form [latex]\dfrac{{\left(y-k\right)}^{2}}{{a}^{2}}-\dfrac{{\left(x-h\right)}^{2}}{{b}^{2}}=1[/latex].
  2. Identify the center of the hyperbola, [latex]\left(h,k\right)[/latex], using the midpoint formula and the given coordinates for the vertices.
  3. Find [latex]{a}^{2}[/latex] by solving for the length of the transverse axis, [latex]2a[/latex] , which is the distance between the given vertices.
  4. Find [latex]{c}^{2}[/latex] using [latex]h[/latex] and [latex]k[/latex] found in Step 2 along with the given coordinates for the foci.
  5. Solve for [latex]{b}^{2}[/latex] using the equation [latex]{b}^{2}={c}^{2}-{a}^{2}[/latex].
  6. Substitute the values for [latex]h,k,{a}^{2}[/latex], and [latex]{b}^{2}[/latex] into the standard form of the equation determined in Step 1.
What is the standard form equation of the hyperbola that has vertices at [latex]\left(0,-2\right)[/latex] and [latex]\left(6,-2\right)[/latex] and foci at [latex]\left(-2,-2\right)[/latex] and [latex]\left(8,-2\right)?[/latex]