Ellipses: Fresh Take

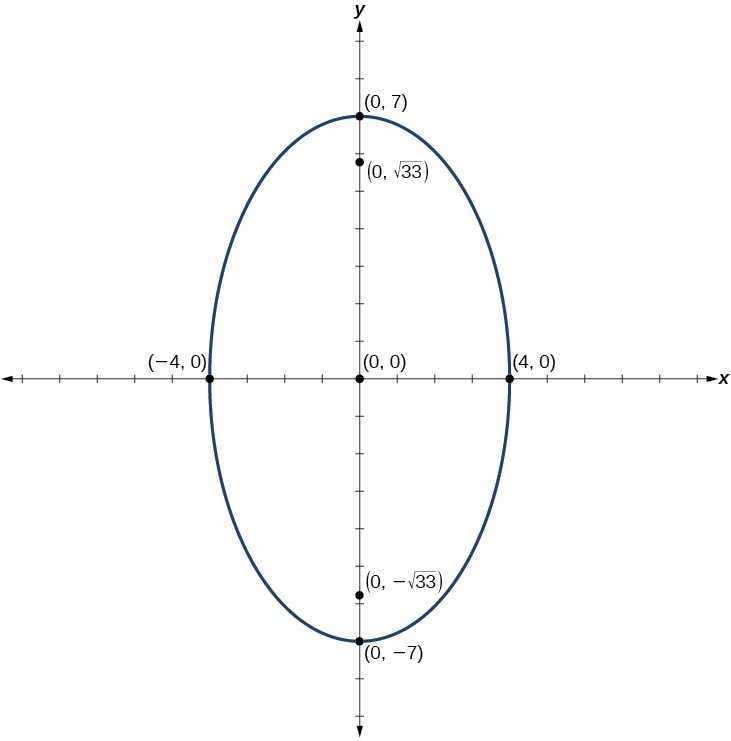
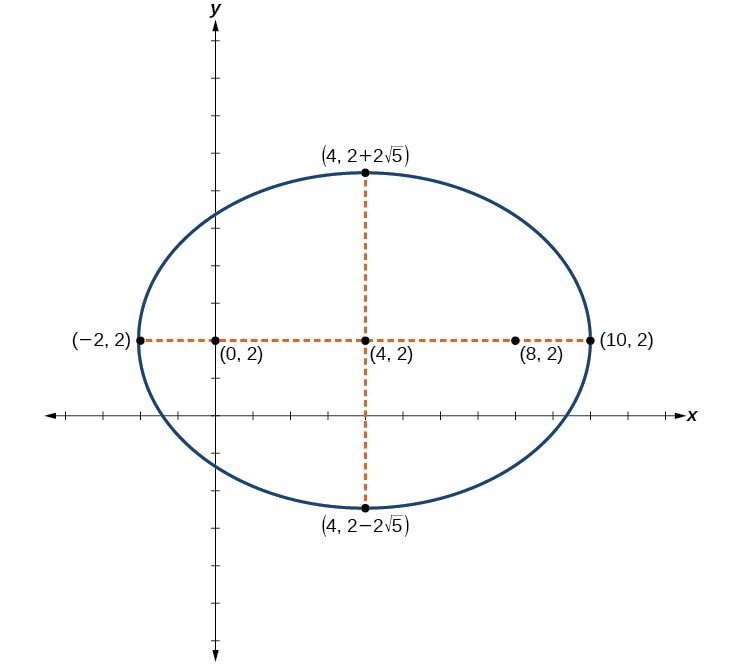
  • Write equations of ellipses in standard form
  • Graph ellipses, understanding how their position changes based on whether they are centered at the origin or at another point
  • Solve applied problems involving ellipses

Ellipses

An ellipse is the set of all points [latex]\left(x,y\right)[/latex] in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci) of the ellipse.We can draw an ellipse using a piece of cardboard, two thumbtacks, a pencil, and string. Place the thumbtacks in the cardboard to form the foci of the ellipse. Cut a piece of string longer than the distance between the two thumbtacks (the length of the string represents the constant in the definition). Tack each end of the string to the cardboard, and trace a curve with a pencil held taut against the string. The result is an ellipse.image

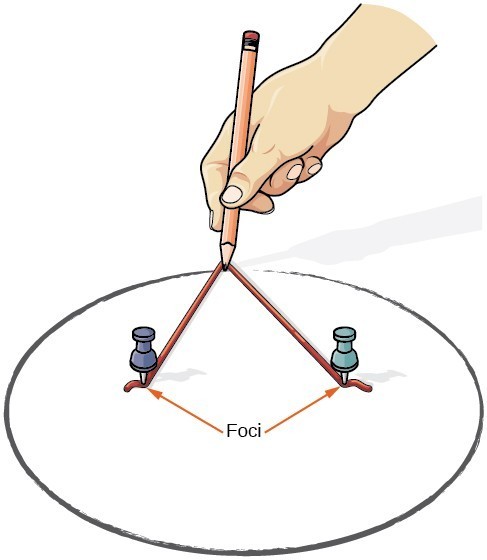
Every ellipse has two axes of symmetry. The longer axis is called the major axis, and the shorter axis is called the minor axis. Each endpoint of the major axis is the vertex of the ellipse (plural: vertices), and each endpoint of the minor axis is a co-vertex of the ellipse. The center of an ellipse is the midpoint of both the major and minor axes. The axes are perpendicular at the center. The foci always lie on the major axis, and the sum of the distances from the foci to any point on the ellipse (the constant sum) is greater than the distance between the foci.

To derive the equation of an ellipse centered at the origin, we begin with the foci [latex](-c,0)[/latex] and [latex](-c,0)[/latex]. The ellipse is the set of all points [latex](x,y)[/latex] such that the sum of the distances from [latex](x,y)[/latex] to the foci is constant, as shown in the figure below.

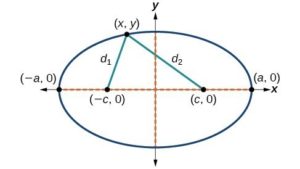
If [latex](a,0)[/latex] is a vertex of the ellipse, the distance from [latex](-c,0)[/latex] to [latex](a,0)[/latex] is [latex]a-(-c)=a+c[/latex]. The distance from [latex](c,0)[/latex] to [latex](a,0)[/latex] is [latex]a-c[/latex]. The sum of the distances from the foci to the vertex is

[latex](a+c)+(a-c)=2a[/latex]

If [latex](x,y)[/latex] is a point on the ellipse, then we can define the following variables:

[latex]\begin{align}d_1&=\text{the distance from } (-c,0) \text{ to } (x,y) \\ d_2&= \text{the distance from } (c,0) \text{ to } (x,y) \end{align}[/latex]

By the definition of an ellipse, [latex]d_1+d_2[/latex] is constant for any point [latex](x,y)[/latex] on the ellipse. We know that the sum of these distances is [latex]2a[/latex] for the vertex [latex](a,0)[/latex]. It follows that [latex]d_1+d_2=2a[/latex] for any point on the ellipse. The derivation of the standard form of the equation of an ellipse relies on this relationship and the distance formula. The derivation is beyond the scope of this course, but the equation is:

[latex]\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1[/latex]

for an ellipse centered at the origin with its major axis on the [latex]x[/latex]-axis and

[latex]\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1[/latex]

for an ellipse centered at the origin with its major axis on the [latex]y[/latex]-axis.

Writing Equations and Graphing Ellipses Centered at the Origin in Standard Form

The Main Idea

  • Standard Forms:
    • Horizontal major axis: [latex]\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1[/latex], where [latex]a > b[/latex]
    • Vertical major axis: [latex]\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1[/latex], where [latex]a > b[/latex]
  • Important Points:
    • Center: Always [latex](0, 0)[/latex] for these forms
    • Vertices: [latex](±a, 0)[/latex] for horizontal, [latex](0, ±a)[/latex] for vertical
    • Co-vertices: [latex](0, ±b)[/latex] for horizontal, [latex](±b, 0)[/latex] for vertical
    • Foci: [latex](±c, 0)[/latex] for horizontal, [latex](0, ±c)[/latex] for vertical, where [latex]c^2 = a^2 - b^2[/latex]
  • Axes Lengths:
    • Major axis: [latex]2a[/latex]
    • Minor axis: [latex]2b[/latex]

From Equation to Graph

  1. Identify orientation (horizontal/vertical) based on larger denominator
  2. Calculate [latex]a[/latex] and [latex]b[/latex] from equation
  3. Find [latex]c[/latex] using [latex]c^2 = a^2 - b^2[/latex]
  4. Plot center, vertices, co-vertices, and foci
  5. Sketch the ellipse through these points

From Points to Equation

  1. Determine orientation from given points
  2. Identify [latex]a[/latex] and [latex]c[/latex] from vertices and foci
  3. Calculate [latex]b[/latex] using [latex]b^2 = a^2 - c^2[/latex]
  4. Substitute values into appropriate standard form
What is the standard form equation of the ellipse that has vertices [latex]\left(0,\pm 8\right)[/latex] and foci [latex](0,\pm \sqrt{5})[/latex]?

Graph the ellipse given by the equation [latex]\dfrac{{x}^{2}}{36}+\dfrac{{y}^{2}}{4}=1[/latex]. Identify and label the center, vertices, co-vertices, and foci.

Graph the ellipse given by the equation [latex]49{x}^{2}+16{y}^{2}=784[/latex]. Rewrite the equation in standard form. Then identify and label the center, vertices, co-vertices, and foci.

You can view the transcript for “Conic Sections: The Ellipse part 2 of 2” here (opens in new window).

You can view the transcript for “Ex 1: Graph an Ellipse with Center at the Origin and Horizontal Major Axis” here (opens in new window).

Writing Equations and Graphing Ellipses Not Centered at the Origin

The Main Idea

  • Standard Forms:
    • Horizontal major axis: [latex]\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1[/latex], where [latex]a > b[/latex]
    • Vertical major axis: [latex]\frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1[/latex], where [latex]a > b[/latex]
  • Key Points:
    • Center: [latex](h, k)[/latex]
    • Vertices: [latex](h ± a, k)[/latex] for horizontal, [latex](h, k ± a)[/latex] for vertical
    • Co-vertices: [latex](h, k ± b)[/latex] for horizontal, [latex](h ± b, k)[/latex] for vertical
    • Foci: [latex](h ± c, k)[/latex] for horizontal, [latex](h, k ± c)[/latex] for vertical, where [latex]c^2 = a^2 - b^2[/latex]
  • Axes Lengths:
    • Major axis: [latex]2a[/latex]
    • Minor axis: [latex]2b[/latex]

From Equation to Graph

  1. Identify orientation (horizontal/vertical) based on larger denominator
  2. Determine center (h, k) from equation
  3. Calculate [latex]a[/latex] and [latex]b[/latex] from equation
  4. Find [latex]c[/latex] using [latex]c^2 = a^2 - b^2[/latex]
  5. Plot center, vertices, co-vertices, and foci
  6. Sketch the ellipse through these points

From Points to Equation

  1. Determine orientation from given points
  2. Find center using midpoint formula
  3. Calculate [latex]a[/latex] (half the distance between vertices)
  4. Find [latex]c[/latex] (distance from center to focus)
  5. Calculate [latex]b[/latex] using [latex]b^2 = a^2 - c^2[/latex]
  6. Substitute values into appropriate standard form
What is the standard form equation of the ellipse that has vertices [latex]\left(-3,3\right)[/latex] and [latex]\left(5,3\right)[/latex] and foci [latex]\left(1 - 2\sqrt{3},3\right)[/latex] and [latex]\left(1+2\sqrt{3},3\right)?[/latex]

Graph the ellipse given by the equation [latex]\dfrac{{\left(x - 4\right)}^{2}}{36}+\dfrac{{\left(y - 2\right)}^{2}}{20}=1[/latex]. Identify and label the center, vertices, co-vertices, and foci.

You can view the transcript for “Ex 1: Graph an Ellipse with Center NOT at the Origin and Horizontal Major Axis” here (opens in new window).

Graphing an Ellipse in General Form

The Main Idea

  • General Form: [latex]ax^2 + by^2 + cx + dy + e = 0[/latex]
  • Goal: Transform to Standard Form [latex]\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1[/latex]
  • Transformation Process:
    • Group like terms
    • Complete the square for [latex]x[/latex] and [latex]y[/latex]
    • Divide by constant term
  • Key Features:
    • Center [latex](h, k)[/latex]
    • Vertices: [latex](h ± a, k)[/latex] or [latex](h, k ± a)[/latex]
    • Co-vertices: [latex](h, k ± b)[/latex] or [latex](h ± b, k)[/latex]
    • Foci: [latex](h ± c, k)[/latex] or [latex](h, k ± c)[/latex], where [latex]c^2 = a^2 - b^2[/latex]
Express the equation of the ellipse given in standard form. Identify the center, vertices, co-vertices, and foci of the ellipse.
[latex]4{x}^{2}+{y}^{2}-24x+2y+21=0[/latex]