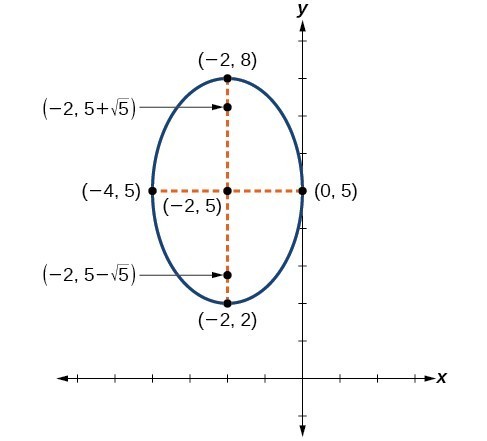
Writing Equations and Graphing Ellipses Not Centered at the Origin
In algebra, we often encounter ellipses centered at the origin, but what if the center is somewhere else? We can handle this by using a transformation.
Imagine shifting the entire coordinate plane so that the new center of the ellipse is at a point [latex](h,k)[/latex]. This horizontal and vertical shift changes the equation of the ellipse to account for its new position. Remember that when we shift horizontally, the [latex]x^2[/latex] term becomes [latex](x-h)^2[/latex], and when we shift vertically, the [latex]y^2[/latex] term becomes [latex](y-k)^2[/latex]. This allows us to easily find the new center, vertices, co-vertices, and foci as well.
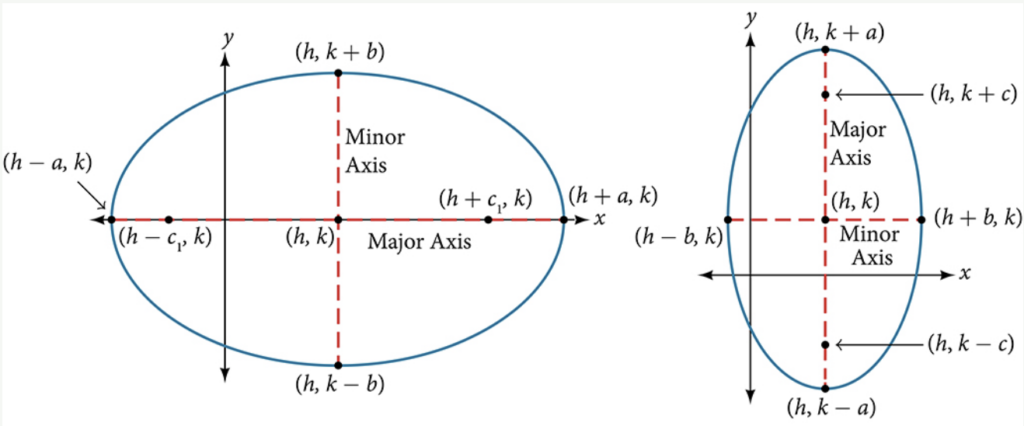
standard forms of the equation of an ellipse with center [latex](h, k)[/latex]
The standard form of the equation of an ellipse with center [latex]\left(h,\text{ }k\right)[/latex] and major axis parallel to the [latex]x[/latex]-axis is
[latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex]
where
- [latex]a>b[/latex]
- the length of the major axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(h\pm a,k\right)[/latex]
- the length of the minor axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(h,k\pm b\right)[/latex]
- the coordinates of the foci are [latex]\left(h\pm c,k\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
The standard form of the equation of an ellipse with center [latex]\left(h,k\right)[/latex] and major axis parallel to the [latex]y[/latex]-axis is
[latex]\dfrac{{\left(x-h\right)}^{2}}{{b}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{a}^{2}}=1[/latex]
where
- [latex]a>b[/latex]
- the length of the major axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(h,k\pm a\right)[/latex]
- the length of the minor axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(h\pm b,k\right)[/latex]
- the coordinates of the foci are [latex]\left(h,k\pm c\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
Just as with ellipses centered at the origin, ellipses that are centered at a point [latex]\left(h,k\right)[/latex] have vertices, co-vertices, and foci that are related by the equation [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex]. We can use this relationship along with the midpoint and distance formulas to find the equation of the ellipse in standard form when the vertices and foci are given.
- Determine whether the major axis is parallel to the [latex]x[/latex]– or [latex]y[/latex]-axis.
- If the [latex]y[/latex]-coordinates of the given vertices and foci are the same, then the major axis is parallel to the [latex]x[/latex]-axis. Use the standard form [latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex].
- If the [latex]x[/latex]-coordinates of the given vertices and foci are the same, then the major axis is parallel to the [latex]y[/latex]-axis. Use the standard form [latex]\dfrac{{\left(x-h\right)}^{2}}{{b}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{a}^{2}}=1[/latex].
- Identify the center of the ellipse [latex]\left(h,k\right)[/latex] using the midpoint formula and the given coordinates for the vertices.
- Find [latex]{a}^{2}[/latex] by solving for the length of the major axis, [latex]2a[/latex], which is the distance between the given vertices.
- Find [latex]{c}^{2}[/latex] using [latex]h[/latex] and [latex]k[/latex], found in Step 2, along with the given coordinates for the foci.
- Solve for [latex]{b}^{2}[/latex] using the equation [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
- Substitute the values for [latex]h,k,{a}^{2}[/latex], and [latex]{b}^{2}[/latex] into the standard form of the equation determined in Step 1.
When an ellipse is not centered at the origin, we can still use the standard forms to find the key features of the graph. When the ellipse is centered at some point, [latex]\left(h,k\right)[/latex], we use the standard forms [latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1,\text{ }a>b[/latex] for horizontal ellipses and [latex]\dfrac{{\left(x-h\right)}^{2}}{{b}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{a}^{2}}=1,\text{ }a>b[/latex] for vertical ellipses. From these standard equations, we can easily determine the center, vertices, co-vertices, foci, and positions of the major and minor axes.
- Use the standard forms of the equations of an ellipse to determine the center, position of the major axis, vertices, co-vertices, and foci.
- If the equation is in the form [latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex], where [latex]a>b[/latex], then
- the center is [latex]\left(h,k\right)[/latex]
- the major axis is parallel to the [latex]x[/latex]-axis
- the coordinates of the vertices are [latex]\left(h\pm a,k\right)[/latex]
- the coordinates of the co-vertices are [latex]\left(h,k\pm b\right)[/latex]
- the coordinates of the foci are [latex]\left(h\pm c,k\right)[/latex]
- If the equation is in the form [latex]\dfrac{{\left(x-h\right)}^{2}}{{b}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{a}^{2}}=1[/latex], where [latex]a>b[/latex], then
- the center is [latex]\left(h,k\right)[/latex]
- the major axis is parallel to the [latex]y[/latex]-axis
- the coordinates of the vertices are [latex]\left(h,k\pm a\right)[/latex]
- the coordinates of the co-vertices are [latex]\left(h\pm b,k\right)[/latex]
- the coordinates of the foci are [latex]\left(h,k\pm c\right)[/latex]
- If the equation is in the form [latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex], where [latex]a>b[/latex], then
- Solve for [latex]c[/latex] using the equation [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
- Plot the center, vertices, co-vertices, and foci in the coordinate plane, and draw a smooth curve to form the ellipse.