• Write equations of ellipses in standard form
• Graph ellipses, understanding how their position changes based on whether they are centered at the origin or at another point
• Solve applied problems involving ellipses

Ellipses

Can you imagine standing at one end of a large room and still being able to hear a whisper from a person standing at the other end? The National Statuary Hall in Washington, D.C. is such a room.^[1] It is an oval-shaped room called a whispering chamber because the shape makes it possible for sound to travel along the walls. The oval-shaped room is called an ellipse, and it is this unique shape that allows sound to travel along the walls.

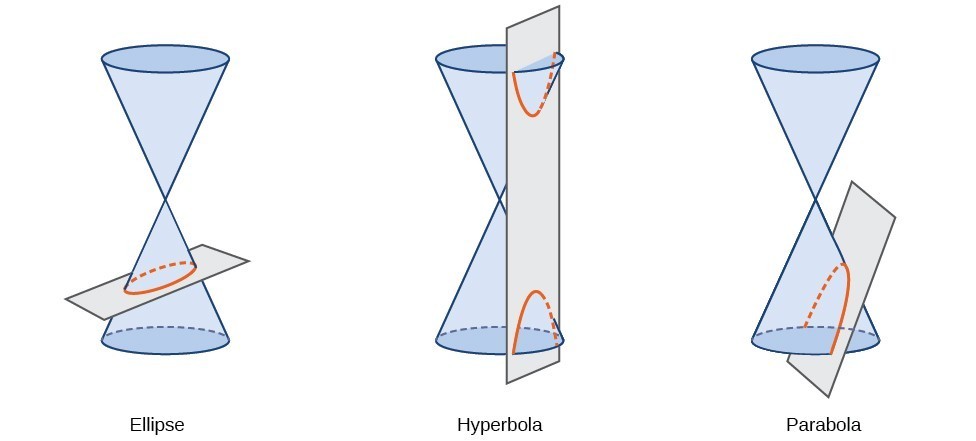
A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines the shape.

Conic sections can also be described by a set of points in the coordinate plane. Later in this chapter we will see that the graph of any quadratic equation in two variables is a conic section. The signs of the equations and the coefficients of the variable terms determine the shape. This section focuses on the four variations of the standard form of the equation for the ellipse. An ellipse is the set of all points [latex]\left(x,y\right)[/latex] in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci) of the ellipse.

The angle at which the plane intersects the cone determines the shape. When the plane intersects the cone at an angle, but not steep enough to reach the base of the cone, the resulting shape is an ellipse. If we pull out the cross section from the figure on the right, we will get an ellipse.

Here are some key characteristics:

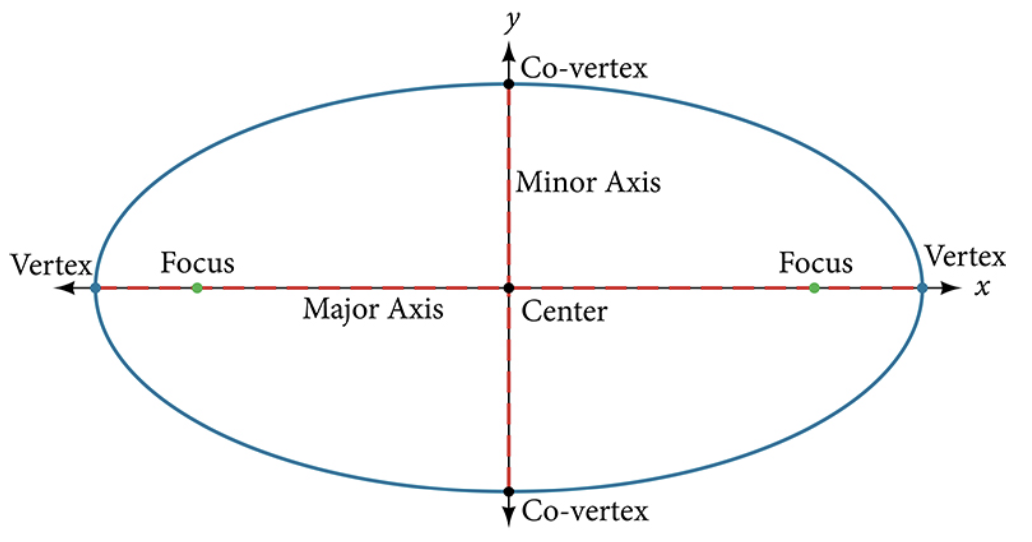
• Every ellipse has two axes of symmetry. The longer axis is called the major axis, and the shorter axis is called the minor axis.
• Each endpoint of the major axis is the vertex of the ellipse (plural: vertices), and each endpoint of the minor axis is a co-vertex of the ellipse.
• The center of an ellipse is the midpoint of both the major and minor axes. The axes are perpendicular at the center.
• The foci always lie on the major axis, and the sum of the distances from the foci to any point on the ellipse (the constant sum) is greater than the distance between the foci.

ellipse

An ellipse is a geometric shape that looks like a stretched-out circle.

An ellipse is the set of all points [latex]\left(x,y\right)[/latex] in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci) of the ellipse.

---