- Write the equations for circles using the standard form
- Graph a circle
- Solve system of equations involving circles
Write the Equation of a Circle in Standard Form
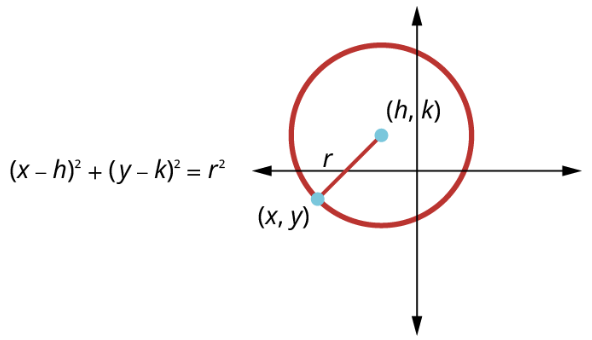
A circle is one of the most familiar shapes in geometry. It’s defined as the set of all points in a plane that are the same distance from a given point in the plane. The given point is called the center, [latex](h,k)[/latex], and the fixed distance is called the radius, [latex]r[/latex], of the circle.
equation of a circle
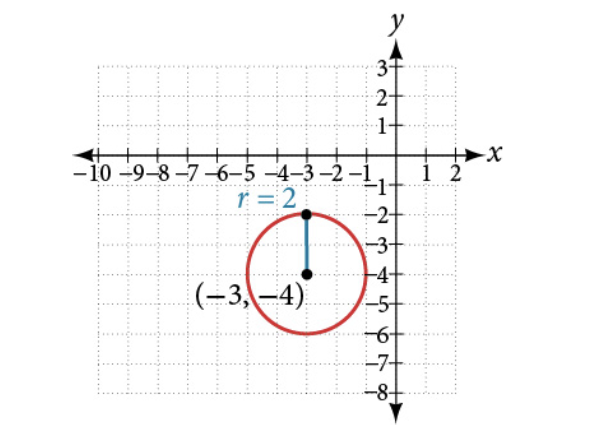
The standard form of the equation of a circle with center at [latex](h,k)[/latex] and radius [latex]r[/latex] is:
[latex](x-h)^2+(y-k)^2 = r^2[/latex]
- radius [latex]3[/latex] and center [latex](0,0)[/latex].
- radius [latex]2[/latex] and center [latex](-1,3)[/latex].
Graph a Circle
Graphing a circle involves a few key steps that build upon our understanding of the standard form equation [latex](x-h)^2+(y-k)^2 = r^2[/latex]. Let’s break down the process.
- Identify the Center and Radius
- The center is given by the point [latex](h,k)[/latex].
- The radius is the square root of the right side of the equation, [latex]r[/latex].
- Plot the Center
- Locate and mark the point [latex](h,k)[/latex] on the coordinate plane.
- Draw the Radius
- From the center, measure [latex]r[/latex] units in all directions.
- You can do this by measuring [latex]r[/latex] units right, left, up, and down from the center.
- Complete the Circle
- Connect the points to form a smooth, round shape.
- Check Key Points
- Verify the four points where the circle intersects the axes:
- [latex](h+r,k)[/latex], [latex](h-r,k)[/latex], [latex](h,k+r)[/latex], and [latex](h,k-r)[/latex]
- Verify the four points where the circle intersects the axes:
[latex](x+3)^2 + (y+4)^2 = 4[/latex]