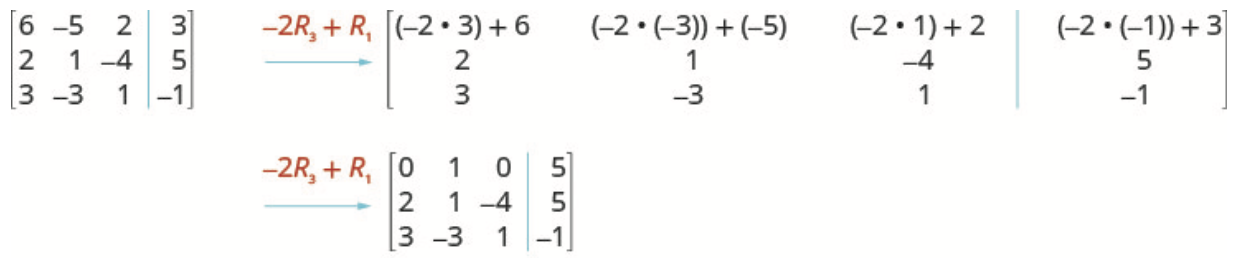Row Operations

Now that we can write systems of equations in augmented matrix form, we will examine the various row operations that can be performed on a matrix, such as addition, multiplication by a constant, and interchanging rows. Performing row operations on a matrix is the method we use for solving a system of equations.

When solving systems of equations using matrices, our goal is to transform the matrix into a simpler form while maintaining the same solution. Row operations help us do this systematically. Think of it like simplifying an equation – we can perform certain operations that don’t change the solution but make it easier to solve.

In a matrix, the following operations can be performed on any row and the resulting matrix will be equivalent to the original matrix.

1. Interchange any two rows.
2. Multiply a row by any real number except [latex]0[/latex].
3. Add a nonzero multiple of one row to another row.

These actions are called row operations and will help us use the matrix to solve a system of equations.

When we perform row operations, we use special notation to show what we’re doing. Here are the common notations you’ll see:

For swapping rows:

• [latex]R_i \leftrightarrow R_j[/latex] means we swap row [latex]i[/latex] and row [latex]j[/latex]

For multiplying a row by a constant:

• [latex]cR_i[/latex] or [latex]R_i \rightarrow cR_i[/latex] means we multiply row [latex]i[/latex] by the constant [latex]c[/latex]
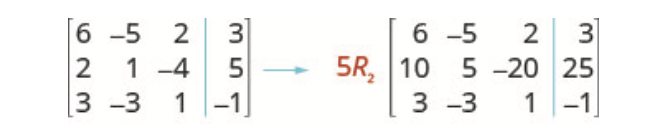
• Example: [latex]5R_2 \rightarrow R_2[/latex] means multiply row [latex]2[/latex] by [latex]5[/latex]

For adding multiples of rows:

• [latex]cR_i + R_j \rightarrow R_j[/latex] means we multiply row [latex]i[/latex] by [latex]c[/latex] and add it to row [latex]j[/latex]
• [latex]R_j \rightarrow R_j + cR_i[/latex] is another common way to write this
• Example: [latex]-3R_3 + R_1 \rightarrow R_1[/latex] means multiply row [latex]3[/latex] by [latex]-3[/latex] and add to row [latex]1[/latex]

These operations can be combined and will be used throughout our work with matrices to solve systems of equations.

Use the indicated row operations on the augmented matrix:[latex]\left[\begin{array}{ccc|c}\hfill 6& \hfill -5& \hfill 2& \hfill 3\\ \hfill 1& \hfill 1& \hfill -4& \hfill 5\\ \hfill 3& \hfill -3& \hfill 1& \hfill -1\\ \end{array}\right][/latex]

1. Interchange rows [latex]2[/latex] and [latex]3[/latex].
   Show Answer

   
2. Multiply row [latex]2[/latex] by [latex]5[/latex].
   Show Answer

   
3. Multiply row [latex]3[/latex] by [latex]−2[/latex] and add to row [latex]1[/latex].
   Show Answer