- Use the commutative, associative, and distributive properties of numbers to solve math problems.
For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.
Commutative Properties
The commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.
- [latex]\left(-2\right)+7=5\text{ and }7+\left(-2\right)=5[/latex]
- [latex]\left(-11\right)\cdot\left(-4\right)=44\text{ and }\left(-4\right)\cdot\left(-11\right)=44[/latex]
It is important to note that neither subtraction nor division is commutative.
Non-examples:
- [latex]17 - 5[/latex] is not the same as [latex]5 - 17[/latex].
- [latex]20\div 5\ne 5\div 20[/latex].
Associative Properties
The associative property of addition tells us that numbers may be grouped differently without affecting the sum.
- [latex]\left(3\cdot4\right)\cdot5=60\text{ and }3\cdot\left(4\cdot5\right)=60[/latex]
- [latex][15+\left(-9\right)]+23=29\text{ and }15+[\left(-9\right)+23]=29[/latex]
Non-examples:
-
[latex]\begin{align}8-\left(3-15\right) & \stackrel{?}{=}\left(8-3\right)-15 \\ 8-\left(-12\right) & \stackrel{?}=5-15 \\ 20 & \neq 20-10 \\ \text{ }\end{align}[/latex]
-
[latex]\begin{align}64\div\left(8\div4\right)&\stackrel{?}{=}\left(64\div8\right)\div4 \\ 64\div2 & \stackrel{?}{=}8\div4 \\ 32 & \neq 2 \\ \text{ }\end{align}[/latex]
Note: neither subtraction nor division is associative.
Distributive Property
This property combines both addition and multiplication (and is the only property to do so).
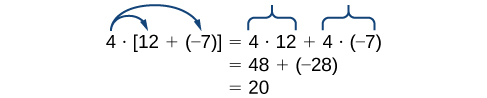
Non-example:
[latex]\begin{align} 6+\left(3\cdot 5\right)& \stackrel{?}{=} \left(6+3\right)\cdot \left(6+5\right) \\ 6+\left(15\right)& \stackrel{?}{=} \left(9\right)\cdot \left(11\right) \\ 21& \ne 99 \end{align}[/latex]
Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.
A special case of the distributive property occurs when a sum of terms is subtracted.
[latex]\\[/latex]
We can rewrite the difference of the two terms [latex]12[/latex] and [latex]\left(5+3\right)[/latex] by turning the subtraction expression into addition of the opposite. So instead of subtracting [latex]\left(5+3\right)[/latex], we add the opposite.
Now, distribute [latex]-1[/latex] and simplify the result.
This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.