Systems of Linear Equations: Two Variables: Learn It 2

Solving Systems of Equations by Graphing

There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.

How to: Solve a system of linear equations by graphing

  1. Graph the first equation.
  2. Graph the second equation on the same rectangular coordinate system.
  3. Determine whether the lines intersect, are parallel, or are the same line.
  4. Identify the solution to the system.
  5. Check the solution in both equations.
Making a quick sketch of any mathematical situation is often a good idea to help you visualize it. Recall the techniques for graphing linear equations include using the y-intercept and slope to plot two points as well as using the intercepts. With practice, you’ll get a feel for which technique to use in a given situation.
Solve the following system of equations by graphing. Identify the type of system.

[latex]\begin{align}2x+y&=-8\\ x-y&=-1\end{align}[/latex]

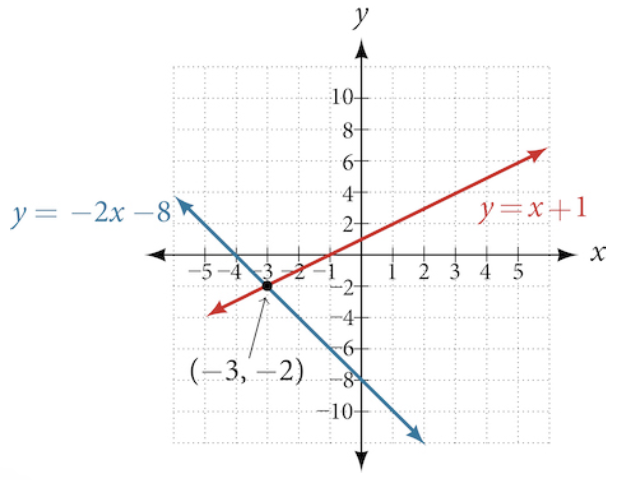
To find the solution, we want to graph both equations on the same set of axes:

  • Solve the first equation for [latex]y[/latex].

[latex]\begin{align}2x+y&=-8\\ y&=-2x-8\end{align}[/latex]

  • Solve the second equation for [latex]y[/latex].

[latex]\begin{align}x-y&=-1\\ y&=x+1\end{align}[/latex]

The lines appear to intersect at the point [latex]\left(-3,-2\right)[/latex].

You can check to make sure that this is the solution to the system by substituting the ordered pair into both equations.

[latex]\begin{align*} 2(-3) + (-2) &= -8 & \text{} \\ -8 &= -8 & \text{True} \\ (-3) - (-2) &= -1 & \text{} \\ -1 &= -1 & \text{True} \end{align*}[/latex]

The solution to the system is the ordered pair [latex]\left(-3,-2\right)[/latex], so the system is independent.

Can graphing be used if the system is inconsistent or dependent?

Yes, in both cases we can still graph the system to determine the type of system and solution.

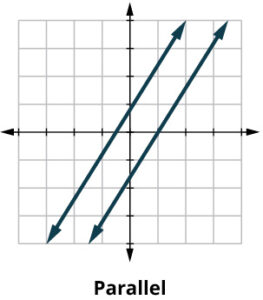
  • If the two lines are parallel, the system has no solution and is inconsistent.
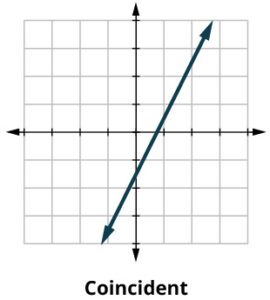
  • If the two lines are identical, the system has infinite solutions and is a dependent system.
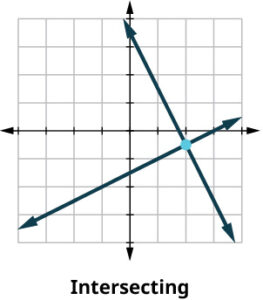
If the lines intersect, identify the point of intersection. This is the solution to the system. Two intersecting lines with a point where the lines cross
If the lines are parallel, the system has no solutions. Two parallel lines
If the lines are the same, the system has an infinite number of solutions. A single line on a graph with the label coincident
Plot the three different systems with an online graphing calculator. Categorize each solution as either consistent or inconsistent. If the system is consistent determine whether it is dependent or independent.

    1. [latex]5x-3y = -19[/latex]
      [latex]x=2y-1[/latex]
    2. [latex]4x+y=11[/latex]
      [latex]-2y=-25+8x[/latex]
    3. [latex]y = -3x+6[/latex]
      [latex]-\frac{1}{3}y+2=x[/latex]

Hint: You may find it easier to plot each system individually, then clear out your entries before you plot the next.