• Convert between logarithmic and exponential forms
• Evaluate logarithms
• Use common and natural logarithms

Real World Scenario

In 2010, a major earthquake struck Haiti destroying or damaging over [latex]285,000[/latex] homes.^[1] One year later, another, stronger earthquake devastated Honshu, Japan destroying or damaging over [latex]332,000[/latex] buildings^[2] like those shown in the picture below. Even though both caused substantial damage, the earthquake in 2011 was [latex]100[/latex] times stronger than the earthquake in Haiti. How do we know? The magnitudes of earthquakes are measured on a scale known as the Richter Scale. The Haitian earthquake registered a [latex]7.0[/latex] on the Richter Scale^[3] whereas the Japanese earthquake registered a [latex]9.0[/latex].^[4]

The Richter Scale is a base-ten logarithmic scale. In other words, an earthquake of magnitude [latex]8[/latex] is not twice as great as an earthquake of magnitude [latex]4[/latex]. It is [latex]{10}^{8 - 4}={10}^{4}=10,000[/latex] times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.

In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. For example, suppose the amount of energy released from one earthquake was [latex]500[/latex] times greater than the amount of energy released from another. We want to calculate the difference in magnitude. The equation that represents this problem is [latex]{10}^{x}=500[/latex] where [latex]x[/latex] represents the difference in magnitudes on the Richter Scale. How would we solve for [latex]x[/latex]?

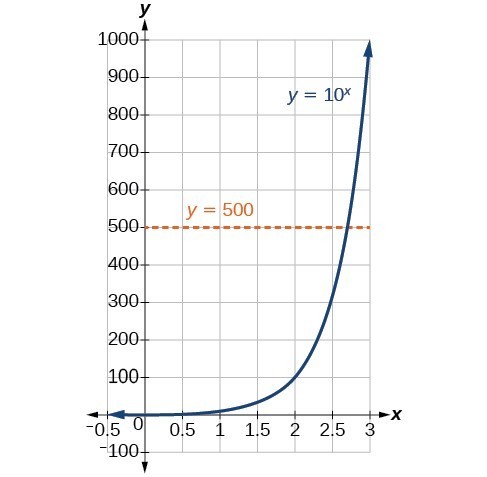
We know that [latex]{10}^{2}=100[/latex] and [latex]{10}^{3}=1000[/latex], so it is clear that [latex]x[/latex] must be some value between [latex]2[/latex] and [latex]3[/latex] since [latex]y={10}^{x}[/latex] is increasing. We can examine a graph to estimate the solution.

We can also use logarithm to solve!

[latex]\begin{align*} 10^x &= 500 \quad \text{(Start with the given equation)} \\ x &= \log_{10}(500) \quad \text{(Rewrite the equation in logarithmic form)} \\ x &= \log(500) \quad \text{(Since $\log_{10}$ is written as $\log$)} \\ x &\approx 2.69897 \quad \text{(Use a calculator to find $\log(500)$)} \end{align*}[/latex]

The magnitude of an earthquake is related to its intensity: for each whole number increase in magnitude, the intensity of the earthquake increases by a factor of [latex]10[/latex]. This means that small differences in Richter Scale measurements can represent massive differences in earthquake intensity.

---