Logarithmic Functions: Learn It 1

  • Convert between logarithmic and exponential forms
  • Evaluate logarithms
  • Use common and natural logarithms

Converting Between Logarithmic And Exponential Form

Have you ever wondered how we can work backward from an exponential equation? That’s where logarithms come in! They are super handy tools that help us solve problems involving exponential functions.

Let’s break it down:
[latex]\\[/latex]
If you know that [latex]2^3 = 8[/latex], you can say that the logarithm base [latex]2[/latex] of [latex]8[/latex] is [latex]3[/latex].In other words:

[latex]{\mathrm{log}}_2(8) = 3[/latex]

A logarithm tells us the power we need to raise a base to get a certain number.

So, when we see [latex]{\mathrm{log}}_2(8) = 3[/latex], it means “to get [latex]8[/latex], what power do we raise [latex]2[/latex] to?” The answer is [latex]3[/latex]!

We can say that the equations [latex]y = {\mathrm{log}}_a(x)[/latex] and [latex]x = a^y[/latex] are equivalent. This means that we can go back and forth between them. This will often be the method to solve some exponential and logarithmic equations. To help with converting back and forth, let’s take a close look at the equations. Notice the positions of the exponent and base.

If we remember the logarithm is the exponent, it makes the conversion easier. You may want to repeat, “base to the exponent gives us the number.”

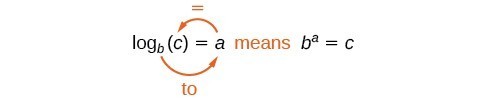
logb (c) = a means b to the A power equals C.

Notice that when comparing the logarithm function and the exponential function, the input and the output are switched. This means [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] and [latex]y={b}^{x}[/latex] are inverse functions.

logarithmic function

A logarithm base [latex]b[/latex] of a positive number [latex]x[/latex] satisfies the following definition:

For [latex]x>0,b>0,b\ne 1[/latex],

 

[latex]y={\mathrm{log}}_{b}\left(x\right)\text{ is equal to }{b}^{y}=x[/latex]

where

  • we read [latex]{\mathrm{log}}_{b}\left(x\right)[/latex] as, “the logarithm with base [latex]b[/latex] of [latex]x[/latex]” or the “log base [latex]b[/latex] of [latex]x[/latex].”
  • the logarithm [latex]y[/latex] is the exponent to which [latex]b[/latex] must be raised to get [latex]x[/latex].
  • if no base [latex]b[/latex] is indicated, the base of the logarithm is assumed to be [latex]10[/latex].

Also, since the logarithmic and exponential functions switch the [latex]x[/latex] and [latex]y[/latex] values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore,

  • the domain of the logarithm function with base [latex]b \text{ is} \left(0,\infty \right)[/latex].
  • the range of the logarithm function with base [latex]b \text{ is} \left(-\infty ,\infty \right)[/latex].
Can we take the logarithm of a negative number?

No. Because the base of an exponential function is always positive, no power of that base can ever be negative. We can never take the logarithm of a negative number. Also, we cannot take the logarithm of zero. Calculators may output a log of a negative number when in complex mode, but the log of a negative number is not a real number.

How To: Given an equation in logarithmic form [latex]{\mathrm{log}}_{b}\left(x\right)=y[/latex], convert it to exponential form

  1. Examine the equation [latex]y={\mathrm{log}}_{b}x[/latex] and identify [latex]b[/latex], [latex]y[/latex], and [latex]x[/latex].
  2. Rewrite [latex]{\mathrm{log}}_{b}x=y[/latex] as [latex]{b}^{y}=x[/latex].
Write the following logarithmic equations in exponential form.

  1. [latex]{\mathrm{log}}_{6}\left(\sqrt{6}\right)=\frac{1}{2}[/latex]
  2. [latex]{\mathrm{log}}_{3}\left(9\right)=2[/latex]

To convert from exponential to logarithmic form, we follow the same steps in reverse. We identify the base [latex]b[/latex], exponent [latex]x[/latex], and output [latex]y[/latex]. Then we write [latex]x={\mathrm{log}}_{b}\left(y\right)[/latex].
Write the following exponential equations in logarithmic form.

  1. [latex]{2}^{3}=8[/latex]
  2. [latex]{5}^{2}=25[/latex]
  3. [latex]{10}^{-4}=\frac{1}{10,000}[/latex]