- Understand what exponential functions are and learn their main features
- Write the equation for an exponential function
- Draw graphs of exponential functions
- Modify graphs of exponential functions using shifts, stretches, and reflections
Defining Exponential Functions
The Main Idea
- Exponential Growth and Decay:
- Exponential growth: Increase based on a constant multiplicative rate over equal time increments
- Exponential decay: Decrease based on a constant multiplicative rate over equal time increments
- Contrast with Linear Growth:
- Exponential: Changes by the same percentage over equal increments
- Linear: Changes by the same amount over equal increments
- General Form of Exponential Function:
- [latex]f(x) = ab^x[/latex]
- [latex]a[/latex] is any nonzero number
- [latex]b[/latex] is a positive real number, [latex]b \neq 1[/latex]
- If [latex]b > 1[/latex]: function grows
- If [latex]0 < b < 1[/latex]: function decays
- Evaluating Exponential Functions:
- Substitute the given value for [latex]x[/latex]
- Follow the order of operations carefully
Which of the following equations represent exponential functions?
- [latex]f(x) = 2x^2 - 3x + 1[/latex]
- [latex]g(x) = 0.875^x[/latex]
- [latex]h(x) = 1.75x + 2[/latex]
- [latex]j(x) = 1095.6^{2x}[/latex]
You can view the transcript for “Introduction to Exponential Functions – Nerdstudy” here (opens in new window).
Exponential Growth and Decay
The Main Idea
- Exponential Growth:
- Output increases by a constant factor over equal intervals
- General form: [latex]f(x) = ab^x[/latex], where [latex]b > 1[/latex]
- Example: [latex]f(x) = 2^x[/latex]
- Exponential Decay:
- Output decreases by a constant factor over equal intervals
- General form: [latex]f(x) = ab^x[/latex], where [latex]0 < b < 1[/latex]
- Example: [latex]g(x) = (\frac{1}{2})^x[/latex]
- Key Characteristics of Exponential Functions:
- Domain: [latex](-\infty, \infty)[/latex]
- Range: [latex](0, \infty)[/latex]
- Horizontal asymptote: [latex]y = 0[/latex]
- [latex]y[/latex]-intercept: [latex](0, 1)[/latex] for [latex]f(x) = b^x[/latex]
- No [latex]x[/latex]-intercept
You can view the transcript for “Exponential growth and decay word problems | Algebra II | Khan Academy” here (opens in new window).
Finding Equations of Exponential Functions
The Main Idea
- General Form of Exponential Functions:
- [latex]f(x) = ab^x[/latex]
- [latex]a[/latex]: initial value
- [latex]b[/latex]: growth factor (if [latex]b > 1[/latex]) or decay factor (if [latex]0 < b < 1[/latex])
- Methods for Finding Equations:
- Using two points
- Using a graph
- Key Principle:
- Every point on the graph satisfies the equation of the function
Problem-Solving Strategies
- When Given Two Points:
- If one point is [latex](0, a)[/latex], use it as the initial value
- If no [latex](0, a)[/latex] point, set up a system of equations
- When Given a Graph:
- Choose the [latex]y[/latex]-intercept as one point if possible
- Select a second point with integer coordinates
- Use points far apart to minimize rounding errors
- General Steps:
- Identify or calculate the initial value [latex]a[/latex]
- Use the second point to solve for [latex]b[/latex]
- Write the equation in the form [latex]f(x) = ab^x[/latex]
You can view the transcript for “Ex: Find an Exponential Function Given Two Points – Initial Value Not Given” here (opens in new window).
You can view the transcript for “Writing Exponential Functions from a Graph” here (opens in new window).
Graphing Exponential Functions
The Main Idea
- Parent Function: [latex]f(x) = b^x[/latex], where [latex]b > 0[/latex] and [latex]b \neq 1[/latex]
- Key Characteristics:
- Domain: All real numbers [latex](-\infty, \infty)[/latex]
- Range: All positive real numbers [latex](0, \infty)[/latex]
- Horizontal asymptote: [latex]y = 0[/latex]
- y-intercept: [latex](0, 1)[/latex]
- No x-intercept
- Growth vs. Decay:
- If [latex]b > 1[/latex]: Exponential growth (increasing function)
- If [latex]0 < b < 1[/latex]: Exponential decay (decreasing function)
Graphing Strategy
- Create a table of points:
- Include negative and positive [latex]x[/latex]-values
- Always include the [latex]y[/latex]-intercept [latex](0, 1)[/latex]
- Plot at least [latex]3[/latex] points, including the y-intercept
- Draw a smooth curve through the points
- Indicate the horizontal asymptote at [latex]y = 0[/latex]
Watch the following video for another example of graphing an exponential function. The base of the exponential term is between [latex]0[/latex] and [latex]1[/latex], so this graph will represent decay.
You can view the transcript for “Graph a Basic Exponential Function Using a Table of Values” here (opens in new window).
The next video example includes graphing an exponential growth function and defining the domain and range of the function.
You can view the transcript for “Graph an Exponential Function Using a Table of Values” here (opens in new window).
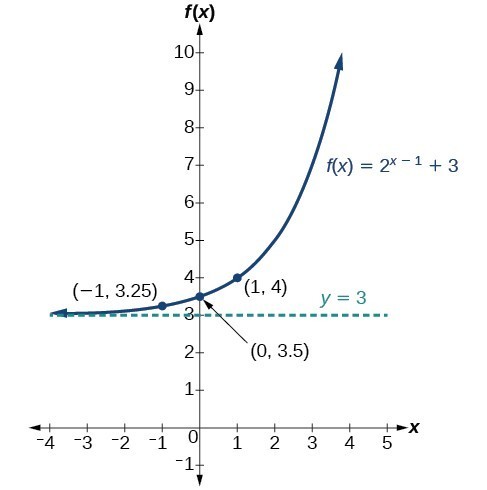
Horizontal and Vertical Translations of Exponential Functions
The Main Idea
- Parent Function: [latex]f(x) = b^x[/latex], where [latex]b > 0[/latex] and [latex]b \neq 1[/latex]
- General Transformed Function: [latex]f(x) = ab^{x-h} + k[/latex]
- [latex]a[/latex]: Vertical stretch/compression
- [latex]h[/latex]: Horizontal shift
- [latex]k[/latex]: Vertical shift
- Key Transformations:
- Vertical Shift: [latex]f(x) = b^x + d[/latex]
- Horizontal Shift: [latex]f(x) = b^{x-c}[/latex]
Transformation Effects
- Vertical Shift ([latex]+d[/latex]):
- Moves graph up [latex]d[/latex] units if [latex]d > 0[/latex], down if [latex]d < 0[/latex]
- Changes [latex]y[/latex]-intercept to [latex](0, 1+d)[/latex]
- Shifts asymptote to [latex]y = d[/latex]
- New range: [latex](d, \infty)[/latex]
- Horizontal Shift ([latex]-c[/latex]):
- Moves graph right [latex]c[/latex] units if [latex]c > 0[/latex], left if [latex]c < 0[/latex]
- Changes [latex]y[/latex]-intercept to [latex](0, b^c)[/latex]
- Asymptote remains at [latex]y = 0[/latex]
- Domain and range unchanged
- Combined Transformations:
- Apply horizontal shift first, then vertical shift
- New [latex]y[/latex]-intercept: [latex](0, b^c + d)[/latex]
- New asymptote: [latex]y = d[/latex]
- New range: [latex](d, \infty)[/latex]
Graphing Strategy
- Identify [latex]b[/latex], [latex]c[/latex], and [latex]d[/latex] in [latex]f(x) = b^{x-c} + d[/latex]
- Draw the horizontal asymptote [latex]y = d[/latex]
- Plot the [latex]y[/latex]-intercept [latex](0, b^c + d)[/latex]
- Sketch the graph, shifting horizontally by [latex]c[/latex] and vertically by [latex]d[/latex]
- State the domain [latex](-\infty, \infty)[/latex], range [latex](d, \infty)[/latex], and asymptote [latex]y = d[/latex]
Watch the following video for more examples of the difference between horizontal and vertical shifts of exponential functions and the resulting graphs and equations.
You can view the transcript for “Ex – Match the Graphs of Translated Exponential Function to Equations_transcript.txt” here (opens in new window).
Stretching, Compressing, or Reflecting an Exponential Function
The Main Idea
- General Transformed Function: [latex]f(x) = ab^{x-h} + k[/latex]
- [latex]a[/latex]: Vertical stretch/compression and reflection
- [latex]b[/latex]: Base of exponential ([latex]b > 0, b \neq 1[/latex])
- [latex]h[/latex]: Horizontal shift
- [latex]k[/latex]: Vertical shift
- Vertical Stretch/Compression:
- [latex]f(x) = ab^x[/latex], where [latex]a \neq 0[/latex]
- Stretch if [latex]|a| > 1[/latex]
- Compress if [latex]0 < |a| < 1[/latex]
- Reflections:
- About [latex]x[/latex]-axis: [latex]f(x) = -b^x[/latex]
- About [latex]y[/latex]-axis: [latex]f(x) = b^{-x}[/latex]
Transformation Effects
- Vertical Stretch/Compression ([latex]a[/latex]):
- Multiplies all [latex]y[/latex]-values by [latex]|a|[/latex]
- New [latex]y[/latex]-intercept: [latex](0, a)[/latex]
- Domain and horizontal asymptote unchanged
- Reflection about [latex]x[/latex]-axis ([latex]-b^x[/latex]):
- Flips graph upside down
- New range: [latex](-\infty, 0)[/latex] if [latex]b > 1[/latex], [latex](0, -\infty)[/latex] if [latex]0 < b < 1[/latex]
- New [latex]y[/latex]-intercept: [latex](0, -1)[/latex]
- Reflection about [latex]y[/latex]-axis ([latex]b^{-x}[/latex]):
- Reverses left-right orientation
- Domain, range, and [latex]y[/latex]-intercept unchanged
- Growth becomes decay (and vice versa)
Graphing Strategy
- Identify [latex]a[/latex], [latex]b[/latex], [latex]h[/latex], and [latex]k[/latex] in [latex]f(x) = ab^{x-h} + k[/latex]
- Apply transformations in this order:
- Horizontal shift
- Reflection about [latex]y[/latex]-axis (if applicable)
- Vertical stretch/compression
- Reflection about [latex]x[/latex]-axis (if applicable)
- Vertical shift
- Plot key points: [latex]y[/latex]-intercept and a few others
- Sketch the curve and asymptote
- State domain, range, and asymptote
- [latex]f\left(x\right)={e}^{x}[/latex] is compressed vertically by a factor of [latex]\frac{1}{3}[/latex], reflected across the [latex]x[/latex]-axis, and then shifted down [latex]2[/latex] units.
You can view the transcript for “Graphing exponential functions with horizontal and vertical transformations” here (opens in new window).
You can view the transcript for “How to Graph Exponential Functions with Transformations (3 Examples)” here (opens in new window).
You can view the transcript for “Ex: Equations of a Transformed Exponential Function” here (opens in new window).