- Learn how to find the inverse (or “reverse”) of a polynomial function when it’s possible
- Figure out how to limit the domain of a polynomial function so you can find its inverse
- Use radical functions to solve real-world problems
Solve Applied Problems Involving Radical Functions
Radical functions are frequently used in real-world applications, especially in physical models where they can describe various natural phenomena. Radical functions often appear in physics, engineering, and biology. They help model situations where relationships between quantities involve roots.
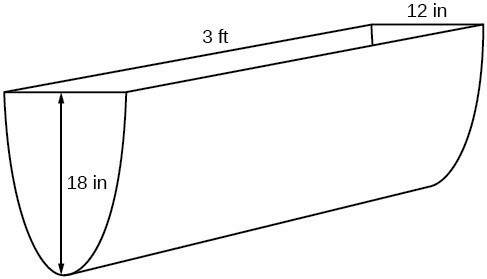
Because it will be helpful to have an equation for the parabolic cross-sectional shape, we will impose a coordinate system at the cross section, with [latex]x[/latex] measured horizontally and [latex]y[/latex] measured vertically, with the origin at the vertex of the parabola.From this we find an equation for the parabolic shape. We placed the origin at the vertex of the parabola, so we know the equation will have form [latex]y\left(x\right)=a{x}^{2}[/latex]. Our equation will need to pass through the point [latex](6, 18)[/latex], from which we can solve for the stretch factor [latex]a[/latex].
[latex]\begin{align} 18&=a{6}^{2} \\[1mm] a&=\frac{18}{36} \\[1mm] a&=\frac{1}{2} \end{align}[/latex]
Our parabolic cross section has the equation
[latex]y\left(x\right)=\frac{1}{2}{x}^{2}[/latex]
We are interested in the surface area of the water, so we must determine the width at the top of the water as a function of the water depth. For any depth [latex]y[/latex] the width will be given by [latex]2x[/latex], so we need to solve the equation above for [latex]x[/latex] and find the inverse function. However, notice that the original function is not one-to-one, and indeed, given any output there are two inputs that produce the same output, one positive and one negative.
To find an inverse, we can restrict our original function to a limited domain on which it is one-to-one. In this case, it makes sense to restrict ourselves to positive [latex]x[/latex] values. On this domain, we can find an inverse by solving for the input variable:
[latex]\begin{align}y&=\frac{1}{2}{x}^{2} \\[1mm] 2y&={x}^{2} \\[1mm] x&=\pm \sqrt{2y} \end{align}[/latex]
This is not a function as written. We are limiting ourselves to positive [latex]x[/latex] values, so we eliminate the negative solution, giving us the inverse function we’re looking for.
[latex]y=\dfrac{{x}^{2}}{2},\text{ }x>0[/latex]
Because [latex]x[/latex] is the distance from the center of the parabola to either side, the entire width of the water at the top will be [latex]2x[/latex]. The trough is [latex]3[/latex] feet ([latex]36[/latex] inches) long, so the surface area will then be:
[latex]\begin{align}\text{Area} &=l\cdot w \\[1mm] &=36\cdot 2x \\[1mm] &=72x \\[1mm] &=72\sqrt{2y} \end{align}[/latex]
[latex]V=\frac{2}{3}\pi {r}^{3}[/latex]
Find the inverse of the function [latex]V=\frac{2}{3}\pi {r}^{3}[/latex] that determines the volume [latex]V[/latex] of a cone and is a function of the radius [latex]r[/latex]. Then use the inverse function to calculate the radius of such a mound of gravel measuring [latex]100[/latex]cubic feet. Use [latex]\pi =3.14[/latex].