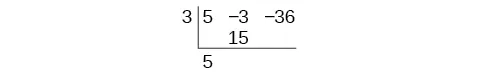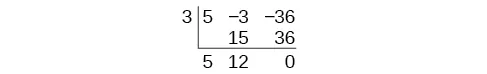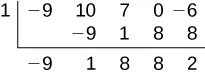Dividing Polynomials: Fresh Take

  • Divide polynomials using the long division method
  • Apply synthetic division as a quicker way to divide polynomials

Polynomial Long Division

The Main Idea 

Polynomial long division might seem daunting at first, but it’s quite similar to the long division we learned in elementary school. Just like we divide numbers, we can divide polynomials, breaking them down into simpler parts. The process involves dividing the highest degree terms and then subtracting to find the remainder, which we then bring down the next term to continue the process.

Quick Tips: Steps to Polynomial Long Division

  1. Set Up: Write the polynomial (dividend) and the binomial (divisor) in long division format.
  2. Divide the Leading Terms: Take the leading term of the dividend and divide it by the leading term of the divisor to find the first term of the quotient.
  3. Multiply and Subtract: Multiply the entire divisor by the term just found and subtract it from the dividend.
  4. Repeat: Bring down the next term of the dividend and repeat the process until you’ve worked through each term.
  5. Remainder: If there’s a remainder, express it as a fraction with the divisor as the denominator.

The Division Algorithm: A Formal ApproachThe Division Algorithm is a fancy way of saying that any polynomial divided by another can be expressed as a multiplication (the quotient) plus something left over (the remainder). It’s a structured method to ensure that every polynomial division can be broken down neatly.

Divide [latex]5{x}^{2}+3x - 2[/latex] by [latex]x+1[/latex].

Divide [latex]16{x}^{3}-12{x}^{2}+20x - 3[/latex] by [latex]4x+5[/latex].

Watch the following video see an example of dividing polynomials with long division.

You can view the transcript for “Dividing polynomials using long division” here (opens in new window).

You can view the transcript for “(New Version Available) Ex 3: Divide a Polynomial by a Binomial Using Long Division” here (opens in new window).

Synthetic Division

The Main Idea 

Synthetic division is a quicker way to divide polynomials when the divisor is a binomial with a leading coefficient of [latex]1[/latex]. It uses only the coefficients of the polynomials, simplifying the process significantly.

How to Use Synthetic Division

  1. Write the Opposite of k: If dividing by [latex]x-k[/latex], write down [latex]k[/latex].
  2. List the Coefficients: Write the coefficients of the polynomial you’re dividing.
  3. Bring Down the Leading Coefficient: This starts off your synthetic division.
  4. Multiply and Add: Multiply the leading coefficient by [latex]k[/latex], add it to the next coefficient, and continue this process.
  5. Find the Quotient and Remainder: The last number is the remainder, and the others form the coefficients of the quotient polynomial.
Use synthetic division to divide [latex]5x^2 - 3x - 36[/latex] by [latex]x - 3[/latex].

Use synthetic division to divide [latex]-9x^4 + 10x^3 + 7x^2 - 6[/latex] by [latex]x - 1[/latex].

Watch the following video see an example of dividing polynomials using synthetic division.

You can view the transcript for “Synthetic Division of Polynomials” here (opens in new window).

You can view the transcript for “Ex 2: Divide a Polynomial by a Binomial Using Synthetic Division” here (opens in new window).