- Divide polynomials using the long division method
- Apply synthetic division as a quicker way to divide polynomials
With your skills in graphing polynomial functions, you can visualize how these functions behave. Now, let’s take it a step further by learning how to divide polynomials. This technique is crucial for breaking down complex polynomials and uncovering their zeros, which are essential for accurate graphing. Did you notice that all of the polynomials we graphed so far are in factored form? We get to this factored form through the process of dividing polynomials.
Dividing polynomials allows us to simplify expressions and find factors that reveal the zeros of the polynomial. These zeros, in turn, help us understand the roots and overall shape of the graph.
Polynomial Long Division
We are familiar with the long division algorithm for ordinary arithmetic. We begin by dividing into the digits of the dividend that have the greatest place value. We divide, multiply, subtract, include the digit in the next place value position, and repeat.

Another way to look at the solution is as a sum of parts. This should look familiar, since it is the same method used to check division in elementary arithmetic.
[latex]\begin{array}{l}\left(\text{divisor }\cdot \text{ quotient}\right)\text{ + remainder}\text{ = dividend}\hfill \\ \left(3\cdot 59\right)+1 = 177+1 = 178\hfill \end{array}[/latex]
We call this the Division Algorithm and will discuss it more formally after looking at an another example.
Division of polynomials that contain more than one term has similarities to long division of whole numbers. We can write a polynomial dividend as the product of the divisor and the quotient added to the remainder. The terms of the polynomial division correspond to the digits (and place values) of the whole number division. This method allows us to divide two polynomials.

We have found
[latex]\frac{2{x}^{3}-3{x}^{2}+4x+5}{x+2}=2{x}^{2}-7x+18-\frac{31}{x+2}[/latex]
or
[latex]2{x}^{3}-3{x}^{2}+4x+5=\left(x+2\right)\left(2{x}^{2}-7x+18\right)-31[/latex]
We can identify the dividend, divisor, quotient, and remainder.
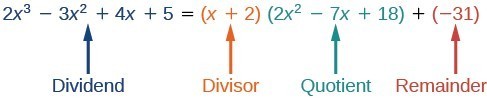
Writing the result in this manner illustrates the Division Algorithm.