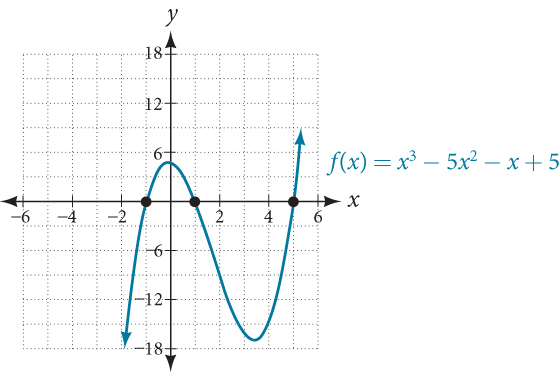
- Identify key features like zeros, turning points, and end behavior in graphs of polynomial functions
- Find where polynomial functions equal zero using different methods, and understand what these zeros mean
- Create and explain graphs of polynomial functions, connecting how the function is written to what its graph looks like
Recognizing Characteristics of Graphs of Polynomial Functions
The Main Idea
- Smoothness: Polynomial functions of degree [latex]2[/latex] or higher have graphs with no sharp corners.
- Continuity: Polynomial graphs have no breaks; they are continuous over their entire domain.
- Domain: All real numbers are valid inputs for polynomial functions.
- Visual Distinction: Polynomial graphs can be distinguished from non-polynomial graphs by their smooth and continuous nature.
- Degree Impact: The degree of the polynomial influences the overall shape and behavior of the graph.
You can view the transcript for “Determining if a graph is a polynomial” here (opens in new window).
Using Factoring to Find Zeros of Polynomial Functions
The Main Idea
- Zeros Definition: Values of [latex]x[/latex] where [latex]f(x) = 0[/latex] for a polynomial function [latex]f[/latex].
- Zeros correspond to [latex]x[/latex]-intercepts of the polynomial’s graph.
- Factoring Methods:
- Using known techniques (e.g., greatest common factor, trinomial factoring)
- Working with pre-factored polynomials
- Utilizing technology for complex cases
- Set each factor to zero and solve for [latex]x[/latex].
- Each linear factor corresponds to a zero of the polynomial.
You can view the transcript for “Finding x and y intercepts given a polynomial function” here (opens in new window).
Identifying Zeros and Their Behavior
The Main Idea
- Zero Definition: Points where a polynomial function crosses or touches the [latex]x[/latex]-axis.
- Multiplicity: The number of times a factor appears in the polynomial’s factored form.
- Behavior at Zeros:
- Odd multiplicity: Graph crosses the [latex]x[/latex]-axis
- Even multiplicity: Graph touches or is tangent to the [latex]x[/latex]-axis
- Degree Relationship: The sum of all zero multiplicities equals the polynomial’s degree.
- Graphical Interpretation: The shape of the graph near a zero indicates its multiplicity.
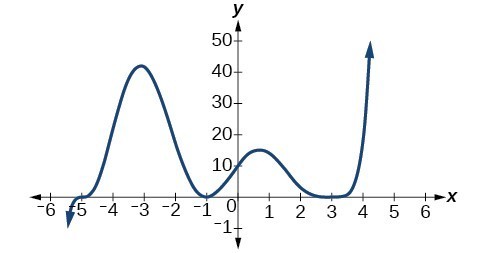
You can view the transcript for “Determine the Zeros/Roots and Multiplicity From a Graph of a Polynomial” here (opens in new window).
Graphing Polynomial Functions
The Main Idea
- Key Elements for Graphing:
- Zeros and their behavior
- [latex]y[/latex]-intercepts
- End behavior
- Local behavior (turning points and concavity)
- Zeros and Their Multiplicities:
- Even multiplicity: Graph touches [latex]x[/latex]-axis
- Odd multiplicity: Graph crosses [latex]x[/latex]-axis
- End Behavior:
- Determined by the degree (odd or even) and sign of the leading coefficient
- Turning Points:
- Maximum number is one less than the polynomial’s degree
- Symmetry:
- Even functions: Symmetric about [latex]y[/latex]-axis
- Odd functions: Symmetric about origin
You can view the transcript for “How to Sketch a Polynomial Function” here (opens in new window).
Using the Intermediate Value Theorem
The Main Idea
- Intermediate Value Theorem (IVT): For a continuous function [latex]f(x)[/latex] on [latex][a,b][/latex], if [latex]y[/latex] is between [latex]f(a)[/latex] and [latex]f(b)[/latex], then there exists a [latex]c[/latex] in [latex][a,b][/latex] where [latex]f(c) = y[/latex].
- Application to Zeros: If [latex]f(a)[/latex] and [latex]f(b)[/latex] have opposite signs, there’s at least one zero between [latex]a[/latex] and [latex]b[/latex].
- Helps prove existence of zeros without directly solving equations.
- Continuity: The theorem relies on the function being continuous.
You can view the transcript for “Intermediate Value Theorem” here (opens in new window).
Writing Formulas for Polynomial Functions
The Main Idea
- Factor Form: [latex]f(x) = a(x-x_1)^{p_1}(x-x_2)^{p_2}...(x-x_n)^{p_n}[/latex]
- [latex]x_i[/latex] are zeros (x-intercepts)
- [latex]p_i[/latex] are multiplicities (behavior at zeros)
- [latex]a[/latex] is the stretch factor
- From Graph to Formula:
- Identify [latex]x[/latex]-intercepts (zeros)
- Determine multiplicity at each zero
- Find stretch factor using another point
Alternative Approaches
- Reverse Engineering:
- Start with simple polynomials and modify them to create desired features.
- Steps:
- a. Begin with a basic polynomial, e.g., [latex]f(x) = x^3[/latex]
- b. Add/subtract a constant to shift vertically: [latex]f(x) = x^3 + 2[/latex]
- c. Add/subtract [latex]x[/latex] to shift horizontally: [latex]f(x) = (x-1)^3 + 2[/latex]
- d. Multiply by a constant to stretch/compress: [latex]f(x) = 2(x-1)^3 + 2[/latex]
- e. Add lower-degree terms to adjust shape: [latex]f(x) = 2(x-1)^3 - 3x + 2[/latex]
- Practice: Start with [latex]f(x) = x^2[/latex] and modify it to match a given graph.
- Technology-Aided Discovery:
- Use graphing calculators or software (e.g., Desmos, GeoGebra) to visualize functions.
- Exploration process:
- a. Input a general polynomial form: [latex]f(x) = ax^3 + bx^2 + cx + d[/latex]
- b. Create sliders for coefficients [latex]a[/latex], [latex]b[/latex], [latex]c[/latex], and [latex]d[/latex]
- c. Adjust sliders to match the given graph
- d. Observe how each coefficient affects the graph’s shape
- Advanced: Use parametric equations to visualize how zeros “move” as coefficients change.
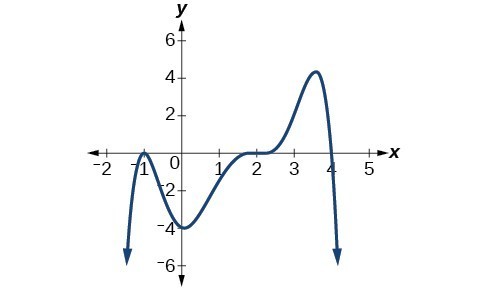
You can view the transcript for “Ex2: Find an Equation of a Degree 5 Polynomial Function From the Graph of the Function” here (opens in new window).
Local and Global Extrema
The Main Idea
- Local Extrema:
- Highest/lowest points in an open interval
- Can be multiple local extrema
- Global Extrema:
- Highest/lowest points on entire function
- Only even-degree polynomials have both
- Turning Points:
- Where function changes from increasing to decreasing or vice versa
- Maximum number: degree of polynomial minus [latex]1[/latex]
You can view the transcript for “Local and Global Extrema” here (opens in new window).