Analysis of Quadratic Functions: Learn It 3

Giselle Miller

Analysis of Quadratic Functions: Learn It 3

Finding Maximum Revenue

Quadratic functions aren’t just abstract math concepts—they’re super useful in real-life situations, especially in business! One cool way we can use quadratic functions is to figure out how to maximize revenue.

Think of it this way: if you’re running a business and selling a product, you want to find the best price to sell that product so you make the most money. Revenue (the money you bring in) is calculated by multiplying the price per unit by the number of units sold. But here’s the catch—the number of units sold usually changes with the price, creating a quadratic relationship.

Let’s see how to use quadratic functions to find that sweet spot—the price that brings in the most revenue! By looking at the graph of the quadratic function, especially the vertex, we can figure out the optimal price to charge.

How To: Given an application involving revenue, use a quadratic equation to find the maximum.

Write a quadratic equation for revenue.
Find the vertex of the quadratic equation.
Determine the [latex]y[/latex]-value of the vertex.

The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease.

A local newspaper currently has [latex]84,000[/latex] subscribers at a quarterly charge of [latex]\$30[/latex]. Market research has suggested that if the owners raise the price to [latex]\$32[/latex], they would lose [latex]5,000[/latex] subscribers.

Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?

Revenue (the money you bring in) is calculated by multiplying the price per unit by the number of units sold.

In this scenario, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity.

Let’s introduce variables: Let [latex]p[/latex] for price per subscription and [latex]Q[/latex] for quantity, giving us the equation [latex]\text{Revenue}=pQ[/latex].

Subscriptions are linearly related to the price. Let’s find the linear function represent the subscription.

Slope

We know that currently [latex]p=30[/latex] and [latex]Q=84,000[/latex]. We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, [latex]p=32[/latex] and [latex]Q=79,000[/latex]. From this we can find a linear equation relating the two quantities. The slope will be

[latex]\begin{align}m&=\dfrac{79,000 - 84,000}{32 - 30} \\ &=\dfrac{-5,000}{2} \\ &=-2,500 \end{align}[/latex]

This tells us the paper will lose 2,500 subscribers for each dollar they raise the price.

[latex]y[/latex]-intercept

[latex]\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}[/latex]

This gives us the linear equation [latex]Q=-2,500p+159,000[/latex] relating cost and subscribers.

Back to the revenue equation.

[latex]\begin{align}&\text{Revenue}=pQ \\ &\text{Revenue}=p\left(-2,500p+159,000\right) \\ &\text{Revenue}=-2,500{p}^{2}+159,000p \end{align}[/latex]

Revenue Function: [latex]R(p) = -2,500{p}^{2}+159,000p[/latex]

We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.

Graph of the parabolic function which the x-axis is labeled Price (p) and the y-axis is labeled Revenue ($). The vertex is at (31.80, 258100).

[latex]\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)} \\ &=31.8 \end{align}[/latex]

The model tells us that the maximum revenue will occur if the newspaper charges [latex]\$31.80[/latex] for a subscription.

To find what the maximum revenue is, we evaluate the revenue function.

[latex]\begin{align}\text{maximum revenue}&=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right) \\ &=\$2,528,100\hfill \end{align}[/latex]

The price should the newspaper charge for a quarterly subscription is [latex]\$31.80[/latex] to obtain the maximum revenue of [latex]\$2,528,100[/latex].

In the example above, we knew the number of subscribers to a newspaper and used that information to find the optimal price for each subscription. What if the price of subscriptions is affected by competition?

Previously, we found a quadratic function that modeled revenue as a function of price.

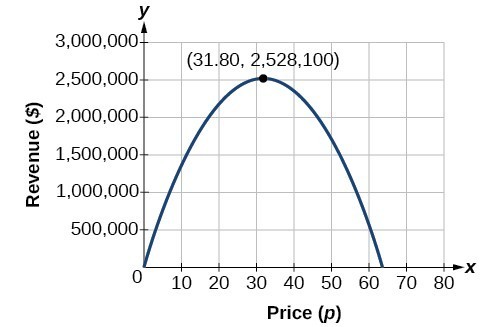
[latex]\text{Revenue}-2,500{p}^{2}+159,000p[/latex]

We found that selling the paper at [latex]\$31.80[/latex] per subscription would maximize revenue. What if your closest competitor sells their paper for [latex]\$25.00[/latex] per subscription? What is the maximum revenue you can make you sell your paper for the same?