- Shift graphs up, down, left, or right to understand how functions move on the coordinate plane
- Flip graphs across the x-axis or y-axis to see how functions mirror themselves
- Look at a graph to decide if a function is symmetrical around the y-axis (even), the origin (odd), or not symmetrical at all
- Apply compressions and stretches to function graphs
- Use different moves and changes like shifting, flipping, squishing, and stretching on graphs
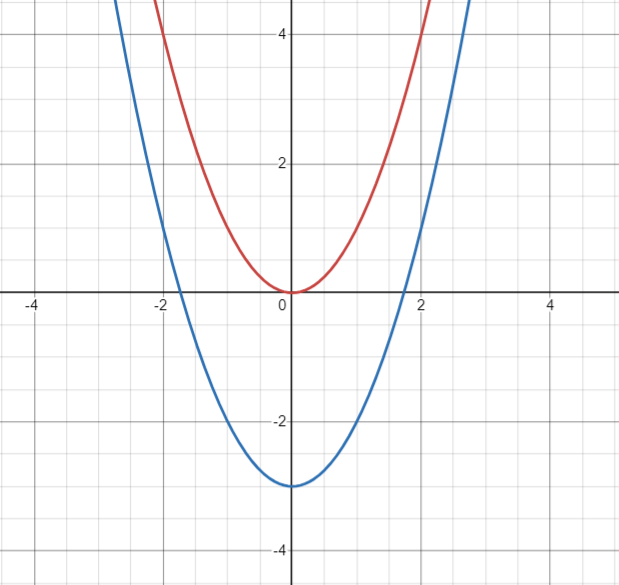
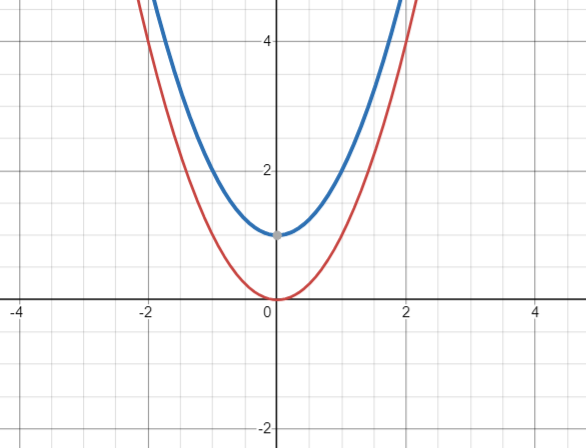
Identifying Vertical Shifts
The Main Idea
- Definition:
- A vertical shift moves a function’s graph up or down without changing its shape
- Achieved by adding or subtracting a constant to the function
- Upward Shift:
- [latex]g(x) = f(x) + c[/latex], where [latex]c > 0[/latex]
- Moves the graph up by [latex]c[/latex] units
- Downward Shift:
- [latex]h(x) = f(x) - c[/latex], where [latex]c > 0[/latex]
- Moves the graph down by [latex]c[/latex] units
- Effect on Function Values:
- Each [latex]y[/latex]-coordinate is increased or decreased by [latex]c[/latex]
- [latex]x[/latex]-coordinates remain unchanged
- Effect on Key Points:
- y-intercept shifts vertically by [latex]c[/latex] units
- Zeros of the function shift vertically (may change number of zeros)
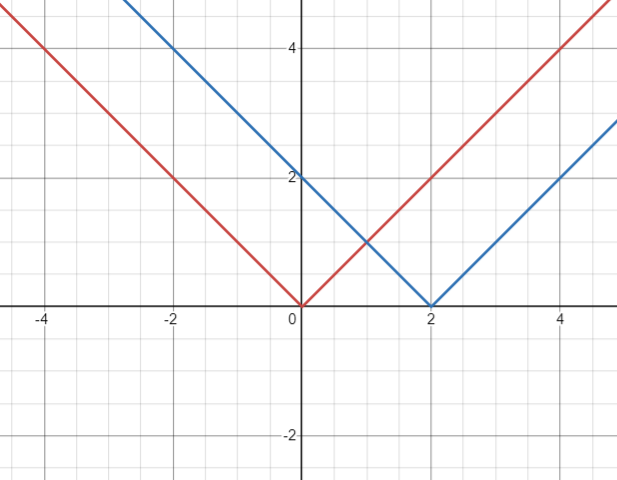
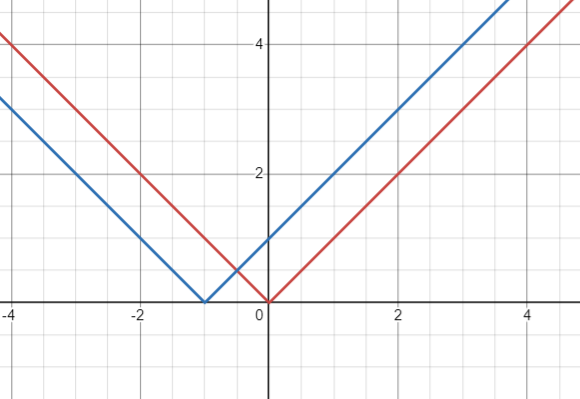
Identifying Horizontal Shifts
The Main Idea
- Definition:
- A horizontal shift moves a function’s graph left or right without changing its shape
- Achieved by adding or subtracting a constant inside the function
- Rightward Shift:
- [latex]g(x) = f(x - c)[/latex], where [latex]c > 0[/latex]
- Moves the graph right by [latex]c[/latex] units
- Leftward Shift:
- [latex]h(x) = f(x + c)[/latex], where [latex]c > 0[/latex]
- Moves the graph left by [latex]c[/latex] units
- Effect on Function Values:
- Each [latex]x[/latex]-coordinate is increased or decreased by [latex]c[/latex]
- [latex]y[/latex]-coordinates remain unchanged
- Effect on Key Points:
- [latex]x[/latex]-intercepts shift horizontally by [latex]c[/latex] units
- [latex]y[/latex]-intercept may change or disappear
Now, enter [latex]f(x+5)[/latex], and [latex]f(x)+5[/latex] in the next two lines.Now have the online graphing calculator make a table of values for the original function. Include integer values on the interval [latex][-5,5][/latex]. Replace the column labeled [latex]y_{1}[/latex] with [latex]f(x_{1})[/latex].Now replace [latex]f(x_{1})[/latex] with [latex]f(x_{1}+3)[/latex], and [latex]f(x_{1})+3[/latex].What are the corresponding functions associated with the transformations you have graphed?
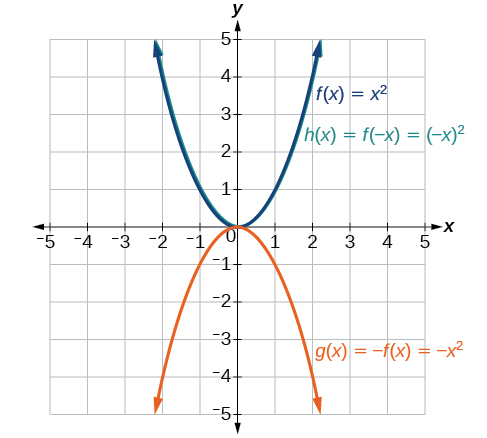
Graphing Functions Using Reflections about the Axes
The Main Idea
- Vertical Reflection:
- Reflects graph across the [latex]x[/latex]-axis
- Changes sign of output: [latex]g(x) = -f(x)[/latex]
- Horizontal Reflection:
- Reflects graph across the [latex]y[/latex]-axis
- Changes sign of input: [latex]g(x) = f(-x)[/latex]
- Effect on Graph:
- Vertical reflection: Mirror image about [latex]x[/latex]-axis
- Horizontal reflection: Mirror image about [latex]y[/latex]-axis
- Domain and Range:
- Reflections can affect the domain and range of functions
- Vertical reflection may change the range
- Horizontal reflection may change the domain
- Composition of Reflections:
- Can be combined with other transformations
- Order of operations matters
| [latex]x[/latex] | −2 | 0 | 2 | 4 |
| [latex]f\left(x\right)[/latex] | 5 | 10 | 15 | 20 |
Using the function [latex]f\left(x\right)[/latex] given in the table above, create a table for the functions below.
a. [latex]g\left(x\right)=-f\left(x\right)[/latex]
b. [latex]h\left(x\right)=f\left(-x\right)[/latex]
Graphing Functions Using Stretches and Compressions
The Main Idea
- Vertical Stretches and Compressions:
- Affect output values: [latex]g(x) = a \cdot f(x)[/latex]
- [latex]a > 1[/latex]: Vertical stretch
- [latex]0 < a < 1[/latex]: Vertical compression
- Horizontal Stretches and Compressions:
- Affect input values: [latex]g(x) = f(b \cdot x)[/latex]
- [latex]0 < b < 1[/latex]: Horizontal stretch by factor [latex]\frac{1}{b}[/latex]
- [latex]b > 1[/latex]: Horizontal compression by factor [latex]\frac{1}{b}[/latex]
- Effect on Graph:
- Vertical: Changes height of graph
- Horizontal: Changes width of graph
- Negative Values:
- [latex]a < 0[/latex]: Combine vertical stretch/compression with reflection over x-axis
- [latex]b < 0[/latex]: Combine horizontal stretch/compression with reflection over y-axis
- Domain and Range:
- Vertical transformations may affect the range
- Horizontal transformations may affect the domain
| [latex]x[/latex] | 2 | 4 | 6 | 8 |
| [latex]f\left(x\right)[/latex] | 12 | 16 | 20 | 0 |
Check your work with an online graphing calculator.
Use an online graphing calculator to check your work.
Performing a Sequence of Transformations
The Main Idea
- Order of Transformations:
- For [latex]y = a \cdot f(b(x-c))+d[/latex], the order is: a. Horizontal shift b. Horizontal stretch/compression c. Reflections d. Vertical stretch/compression e. Vertical shift
- Horizontal Transformations:
- Shift: [latex]f(x-c)[/latex] shifts right by [latex]c[/latex] units
- Stretch/Compression: [latex]f(bx)[/latex] stretches by factor [latex]\frac{1}{b}[/latex]
- Vertical Transformations:
- Shift: [latex]f(x)+d[/latex] shifts up by [latex]d[/latex] units
- Stretch/Compression: [latex]a \cdot f(x)[/latex] stretches by factor [latex]a[/latex]
- Reflections:
- Horizontal: [latex]f(-x)[/latex] reflects across y-axis
- Vertical: [latex]-f(x)[/latex] reflects across x-axis
- Composite Transformations:
- Apply transformations from inside to outside
- Pay attention to the order of operations
Check your work with an online graphing calculator.
You can view the transcript for “Functions Transformations: A Summary” here (opens in new window).
Determine Whether a Functions is Even, Odd, or Neither
The Main Idea
- Even Functions:
- Symmetrical about the y-axis
- [latex]f(x) = f(-x)[/latex] for all x in the domain
- Example: [latex]f(x) = x^2[/latex]
- Odd Functions:
- Symmetrical about the origin
- [latex]f(x) = -f(-x)[/latex] for all x in the domain
- Example: [latex]f(x) = x^3[/latex]
- Neither Even nor Odd:
- Functions that don’t satisfy either condition
- Example: [latex]f(x) = 2^x[/latex]
- Special Cases:
- [latex]f(x) = 0[/latex] is both even and odd
- Polynomial functions with only even powers are even
- Polynomial functions with only odd powers are odd
- Graphical Interpretation:
- Even: Unchanged when reflected over y-axis
- Odd: Unchanged when rotated 180° about the origin
You can view the transcript for “Introduction to Odd and Even Functions” here (opens in new window).