- Use algebraic operations to combine functions and create new expressions
- Build a new function by combining two or more functions together
- Calculate the output for composite functions for given values and determine the set of inputs that work for these functions
- Break down a composite function into the original functions that were combined to make it
Combining Functions Using Algebraic Operations
The Main Idea
- Function Addition:
- [latex](f + g)(x) = f(x) + g(x)[/latex]
- Function Subtraction:
- [latex](f - g)(x) = f(x) - g(x)[/latex]
- Function Multiplication:
- [latex](f \cdot g)(x) = f(x) \cdot g(x)[/latex]
- Function Division:
- [latex]\left(\frac{f}{g}\right)(x) = \frac{f(x)}{g(x)}[/latex], where [latex]g(x) \neq 0[/latex]
- Domain Considerations:
- Resulting function’s domain may be restricted, especially for division
[latex]f\left(x\right)=x - 1\text{ and }g\left(x\right)={x}^{2}-1[/latex]
Are they the same function?
Create a Function by Composition of Functions
The Main Idea
- Definition:
- [latex](f \circ g)(x) = f(g(x))[/latex]
- Read as “f composed with g of x” or “f of g of x”
- Order Matters:
- Generally, [latex](f \circ g)(x) \neq (g \circ f)(x)[/latex]
- Domain Considerations:
- Domain of [latex]f \circ g[/latex]: All [latex]x[/latex] in domain of [latex]g[/latex] where [latex]g(x)[/latex] is in domain of [latex]f[/latex]
- Evaluation Process:
- Work from innermost function outward
- Not Multiplication:
- [latex](f \circ g)(x) \neq (f \cdot g)(x)[/latex]
[latex]f\left(x\right)=2x+1\\g\left(x\right)=3-x[/latex]
You can view the transcript for “Composite Functions” here (opens in new window).
You can view the transcript for “Ex 4: Domain of a Composite Function” here (opens in new window).
Evaluating Composite Functions
The Main Idea
- General Approach:
- Work from inside to outside
- Evaluate inner function first, use result as input for outer function
- Using Tables:
- Read input/output values directly from table entries
- [latex](f \circ g)(x) = f(g(x))[/latex]: Look up [latex]g(x)[/latex], then use result to find [latex]f[/latex] value
- Using Graphs:
- Read input/output values from [latex]x[/latex] and [latex]y[/latex] axes
- Follow points across graphs for composite functions
- Using Formulas:
- Substitute expression for inner function into outer function
- Simplify to get formula for composite function
- Domain Considerations:
- Check domains of both inner and outer functions
- Ensure composition is valid for given input
| [latex]x[/latex] | [latex]f\left(x\right)[/latex] | [latex]g\left(x\right)[/latex] |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 8 | 5 |
| 3 | 3 | 2 |
| 4 | 1 | 7 |
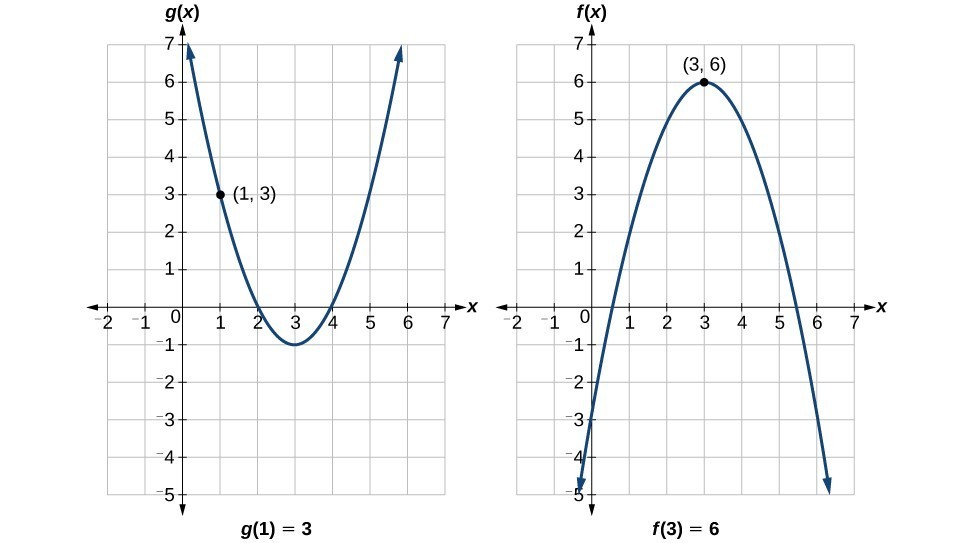
You can view the transcript for “Ex: Evaluate Composite Functions from Graphs” here (opens in new window).
You can view the transcript for “Ex 1: Composite Function Values” here (opens in new window).
Decomposing a Composite Function
The Main Idea
- Definition:
- Breaking down a complex function into simpler component functions
- [latex]f(x) = g(h(x))[/latex], where [latex]g[/latex] and [latex]h[/latex] are simpler functions
- Multiple Solutions:
- There’s often more than one way to decompose a function
- Choose the decomposition that seems most useful or intuitive
- Process:
- Identify a “function inside a function” in the original expression
- Define inner function [latex]h(x)[/latex] and outer function [latex]g(x)[/latex]
- Verification:
- Recompose the functions to check if [latex]g(h(x))[/latex] equals the original function
- Applications:
- Simplifying complex functions
- Understanding function structure
- Solving certain types of equations
You can view the transcript for “Ex: Decompose Functions” here (opens in new window).