- Use algebraic operations to combine functions and create new expressions
- Build a new function by combining two or more functions together
- Calculate the output for composite functions for given values and determine the set of inputs that work for these functions
- Break down a composite function into the original functions that were combined to make it
Understanding Composite Functions
Now that you have learned about composite functions and their domains, let’s interpret what a composite function means.
Composite functions can model real-world scenarios where a series of processes or transformations are applied sequentially.
- The cost depends on the temperature
- the temperature depends on the day
Using descriptive variables, we can notate these two functions.
- The function [latex]C\left(T\right)[/latex] gives the cost [latex]C[/latex] of heating a house for a given average daily temperature in [latex]T[/latex] degrees Celsius.
- The function [latex]T\left(d\right)[/latex] gives the average daily temperature on day [latex]d[/latex] of the year.
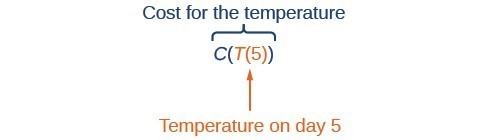
For any given day, [latex]\text{Cost}=C\left(T\left(d\right)\right)[/latex] means that the cost depends on the temperature, which in turns depends on the day of the year. Thus, we can evaluate the cost function at the temperature [latex]T\left(d\right)[/latex].
For example, we could evaluate [latex]T\left(5\right)[/latex] to determine the average daily temperature on the 5th day of the year. Then, we could evaluate the cost function at that temperature. We would write [latex]C\left(T\left(5\right)\right)[/latex].
To interpret [latex]c(s(3))[/latex], follow these steps:
- Identify [latex]s(3)[/latex]: This represents the number of sit-ups a person can complete in [latex]3[/latex] minutes. So, [latex]s(3)[/latex] tells us how many sit-ups are done in [latex]3[/latex] minutes.
- Apply [latex]c[/latex] to [latex]s(3)[/latex]: Once you know the number of sit-ups completed in [latex]3[/latex] minutes (which is [latex]s(3)[/latex], you use the function [latex]c[/latex] to determine how many calories are burned from doing that number of sit-ups.
Thus, [latex]c(s(3))[/latex] represents the number of calories burned from the number of sit-ups that can be completed in [latex]3[/latex] minutes.
In other words, you first calculate how many sit-ups are completed in [latex]3[/latex] minutes, and then determine the calories burned from that amount of exercise.