- Find the average rate of change of a function
- Identify parts of a graph where the function is going up, going down, or staying the same
- Identify the highest and lowest points, both overall and at specific spots, on a graph
Rates of Change
The Main Idea
- Definition:
- Rate of change describes how an output quantity changes relative to the input quantity
- Units: output units per input units
- Average Rate of Change:
- Calculated over an interval
- Formula: [latex]\frac{\Delta y}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1}[/latex]
- Interpretation:
- Positive rate: output increases as input increases
- Negative rate: output decreases as input increases
- Applications:
- Population growth
- Speed (distance per time)
- Fuel efficiency (distance per volume)
- Economic indicators (price changes over time)
Key Techniques
- Calculating Average Rate of Change:
- Identify the interval [latex][x_1, x_2][/latex]
- Calculate change in output: [latex]\Delta y = f(x_2) - f(x_1)[/latex]
- Calculate change in input: [latex]\Delta x = x_2 - x_1[/latex]
- Divide: [latex]\frac{\Delta y}{\Delta x}[/latex]
- Interpreting from Graphs:
- Slope of secant line between two points
- Vertical change divided by horizontal change
- Working with Functions:
- Evaluate function at endpoints of interval
- Apply average rate of change formula
Using the data in the table below, find the average rate of change between 2014 and 2019.
| [latex]y[/latex] | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| [latex]C\left(y\right)[/latex] | 3.358 | 2.429 | 2.143 | 2.415 | 2.719 | 2.604 | 2.168 | 3.008 | 3.951 | 3.519 |
You can view the transcript for “Ex: Find the Average Rate of Change From a Table – Temperatures” here (opens in new window).
You can view the transcript for “Ex: Find the Average Rate of Change Given a Function Rule” here (opens in new window).
Behaviors of Functions
Using a Graph to Determine Where a Function is Increasing, Decreasing, or Constant
The Main Idea
- Increasing and Decreasing Intervals:
- Increasing: function values increase as input increases
- Decreasing: function values decrease as input increases
- Constant: function values remain the same as input increases
- Local Extrema:
- Local Maximum: where function changes from increasing to decreasing
- Local Minimum: where function changes from decreasing to increasing
- Collectively called local extrema or relative extrema
- Graphical Interpretation:
- Increasing: graph slopes upward from left to right
- Decreasing: graph slopes downward from left to right
- Local maximum: highest point in a neighborhood
- Local minimum: lowest point in a neighborhood
- Mathematical Definitions:
- Increasing: [latex]f(b) > f(a)[/latex] for [latex]b > a[/latex] in an interval
- Decreasing: [latex]f(b) < f(a)[/latex] for [latex]b > a[/latex] in an interval
- Local maximum at [latex]x = b[/latex]: [latex]f(x) \leq f(b)[/latex] for all [latex]x[/latex] in some interval containing [latex]b[/latex]
- Local minimum at [latex]x = b[/latex]: [latex]f(x) \geq f(b)[/latex] for all [latex]x[/latex] in some interval containing [latex]b[/latex]
Key Techniques
- Identifying Increasing/Decreasing Intervals:
- Observe graph from left to right
- Note where slope changes from positive to negative or vice versa
- Locating Local Extrema:
- Look for “peaks” (local maxima) and “valleys” (local minima)
- Confirm by checking neighboring points
- Using Technology:
- Utilize graphing calculators or software to visualize functions
- Use built-in features to estimate extrema locations
- Analyzing Complex Functions:
- Break down the graph into smaller intervals
- Analyze behavior within each interval
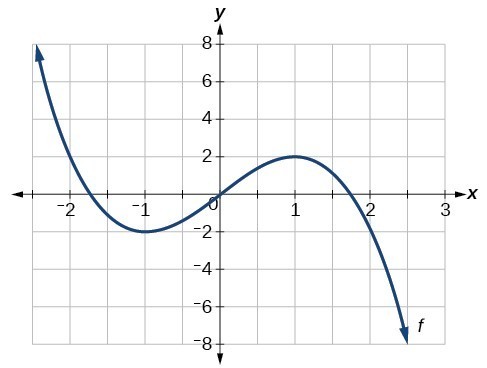
You can view the transcript for “Determine Where a Function is Increasing and Decreasing” here (opens in new window).
Analyzing the Toolkit Functions for Increasing or Decreasing Intervals
The Main Idea
- Constant Function: [latex]f(x) = c[/latex]
- Behavior: Neither increasing nor decreasing
- Graph: Horizontal line
- Identity Function: [latex]f(x) = x[/latex]
- Behavior: Increasing on [latex](-\infty, \infty)[/latex]
- Graph: Straight line through origin
- Quadratic Function: [latex]f(x) = x^2[/latex]
- Increasing: [latex](0, \infty)[/latex]
- Decreasing: [latex](-\infty, 0)[/latex]
- Minimum: At [latex]x = 0[/latex]
- Graph: Parabola opening upward
- Cubic Function: [latex]f(x) = x^3[/latex]
- Behavior: Increasing on [latex](-\infty, \infty)[/latex]
- Graph: S-shaped curve
- Reciprocal Function: [latex]f(x) = \frac{1}{x}[/latex]
- Decreasing: [latex](-\infty, 0) \cup (0, \infty)[/latex]
- Graph: Hyperbola with vertical asymptote at x = 0
- Reciprocal Squared: [latex]f(x) = \frac{1}{x^2}[/latex]
- Increasing: [latex](-\infty, 0)[/latex]
- Decreasing: [latex](0, \infty)[/latex]
- Graph: U-shaped curve with vertical asymptote at x = 0
- Cube Root: [latex]f(x) = \sqrt[3]{x}[/latex]
- Behavior: Increasing on [latex](-\infty, \infty)[/latex]
- Graph: S-shaped curve, less steep than cubic
- Square Root: [latex]f(x) = \sqrt{x}[/latex]
- Increasing: [latex](0, \infty)[/latex]
- Domain: [latex][0, \infty)[/latex]
- Graph: Curve starting at origin, opening upward
- Absolute Value: [latex]f(x) = |x|[/latex]
- Increasing: [latex](0, \infty)[/latex]
- Decreasing: [latex](-\infty, 0)[/latex]
- Minimum: At [latex]x = 0[/latex]
- Graph: V-shaped graph
Use A Graph to Locate the Absolute Maximum and Absolute Minimum
The Main Idea
- Absolute Extrema vs. Local Extrema:
- Absolute: Highest/lowest points over entire domain
- Local: Highest/lowest points in a local region
- Absolute Maximum:
- Highest point on the entire graph
- [latex]f(c)[/latex] is absolute max if [latex]f(c) \geq f(x)[/latex] for all [latex]x[/latex] in domain
- Absolute Minimum:
- Lowest point on the entire graph
- [latex]f(d)[/latex] is absolute min if [latex]f(d) \leq f(x)[/latex] for all [latex]x[/latex] in domain
- Existence of Absolute Extrema:
- Not all functions have absolute extrema
- Example: [latex]f(x) = x^3[/latex] has neither absolute max nor min
Key Techniques
- Graphical Identification:
- Observe entire graph within function’s domain
- Locate highest and lowest points
- Comparing Extrema:
- Compare all local maxima to find absolute maximum
- Compare all local minima to find absolute minimum
- Considering Domain:
- Check domain boundaries for potential absolute extrema
- Be aware of asymptotic behavior
- Multiple Absolute Extrema:
- Functions can have multiple absolute maxima or minima
- These occur at same y-value but different x-values
Consider the function:
[latex]f(x) = \begin{cases} x^2 & \text{if } x < 0 \\ 16 - x^2 & \text{if } 0 \leq x \leq 4 \\ 0 & \text{if } x > 4 \end{cases}[/latex]
Find the absolute maximum and minimum.