Applications of Non-Linear Equations: Learn It 2

Areas and Volumes

  • Perimeter of a rectangle: [latex]P = 2L+2W[/latex]
  • Area of a square: [latex]A = s^2[/latex]
  • Area of a rectangle: [latex]A = lw[/latex]
  • Area of a triangle: [latex]A = \dfrac{1}{2}bh[/latex]
  • Area of a cicle: [latex]A = \pi r^2[/latex]
  • Volume of a box: [latex]V = LWH[/latex]
  • Volume of a sphere: [latex]V = \dfrac{4}{3} \pi r^3[/latex]

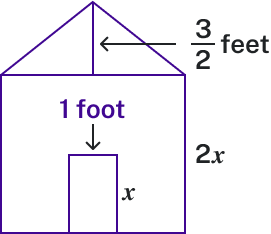
Maahi is building a little free library (a small house-shaped book repository), whose front is in the shape of a square topped with a triangle. There will be a rectangular door through which people can take and donate books. Maahi wants to find the area of the front of the library so that they can purchase the correct amount of paint. Note, Maahi is not painting the door.

Using the measurements of the front of the house, shown below, create an expression that represents the area of the front of the library.

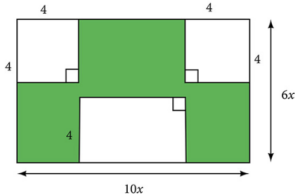
A simple house-shaped diagram drawn in purple. The house has a rectangular base with a triangular roof on top. Inside the rectangular portion is a smaller rectangle that could represent a door. The diagram includes several measurements: the height of the door is labeled as "x", the space above the door to the roof is labeled as "1 foot", the height of the entire rectangular portion is marked as "2x", and a horizontal measurement in the roof area is labeled as "3/2 feet".

Imagine that we are trying to find the area of a lawn so that we can determine how much grass seed to purchase. The lawn is the green portion in the figure below.

Create an expression that represents the area of the region that requires grass seed.

Find the dimensions of a shipping box given that the length is twice the width, the height is  [latex]8[/latex] inches, and the volume is [latex]1600 \text{ in.}^3[/latex].