- Use interval notation to show solutions to inequalities.
- Solve linear inequalities by applying their properties.

Using Interval Notation
In many academic institutions, student performance is evaluated using a Grade Point Average (GPA) system where scores range from [latex]0[/latex] to [latex]4[/latex]. This scale can be represented using linear inequalities to define the complete range of possible GPAs. How could these GPA scores be expressed mathematically?
- Set-Builder Notation: [latex]\{x \mid 0 \leq x \leq 4\}[/latex], where [latex]x[/latex] represents a student’s GPA.
The inequality [latex]0 \leq x \leq 4[/latex] encapsulates the idea that a GPA can be as low as [latex]0[/latex], which might indicate failing grades or no coursework completed, and as high as [latex]4[/latex], representing perfect academic performance. - Interval Notation: [latex][0, 4][/latex].
This notation correctly specifies that the GPA can be any value including and between [latex]0[/latex] and [latex]4[/latex]. - Number Line: The number line below illustrates that the solution set includes all real numbers between [latex]0[/latex] and [latex]4[/latex].

Number line with points on 0 and 4
- Parentheses represent solutions greater or less than the number.
- Brackets represent solutions that are greater than or equal to or less than or equal to the number.
- Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.”
- [latex]<[/latex] (less than)
- [latex]>[/latex] (greater than)
- [latex]\leq[/latex] (less than or equal to)
- [latex]\geq[/latex] (greater than or equal to)
Inequalities show that one side of the statement is not equal to the other. Instead, it describes a range of possible values. For example, the inequality [latex]x > 3[/latex] means that [latex]x[/latex] can be any number greater than 3.
| Inequality | Words | Interval Notation | Number Line |
|---|---|---|---|
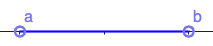
| [latex]{a}\lt{x}\lt{ b}[/latex] | all real numbers between a and b, not including a and b | [latex]\left(a,b\right)[/latex] |
|
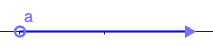
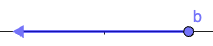
| [latex]{x}\gt{a}[/latex] | All real numbers greater than a, but not including a | [latex]\left(a,\infty \right)[/latex] |
|
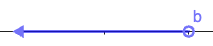
| [latex]{x}\lt{b}[/latex] | All real numbers less than b, but not including b | [latex]\left(-\infty ,b\right)[/latex] |
|
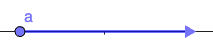
| [latex]{x}\ge{a}[/latex] | All real numbers greater than a, including a | [latex]\left[a,\infty \right)[/latex] |
|
| [latex]{x}\le{b}[/latex] | All real numbers less than b, including b | [latex]\left(-\infty ,b\right][/latex] |
|
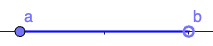
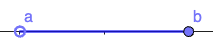
| [latex]{a}\le{x}\lt{ b}[/latex] | All real numbers between a and b, including a | [latex]\left[a,b\right)[/latex] |
|
| [latex]{a}\lt{x}\le{ b}[/latex] | All real numbers between a and b, including b | [latex]\left(a,b\right][/latex] |
|
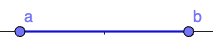
| [latex]{a}\le{x}\le{ b}[/latex] | All real numbers between a and b, including a and b | [latex]\left[a,b\right][/latex] |
|
| [latex]{x}\lt{a}\text{ or }{x}\gt{ b}[/latex] | All real numbers less than a or greater than b | [latex]\left(-\infty ,a\right)\cup \left(b,\infty \right)[/latex] |
|
| All real numbers | All real numbers | [latex]\left(-\infty ,\infty \right)[/latex] |
|
- All real numbers greater than or equal to [latex]-2[/latex].
- All real numbers between and including [latex]-3[/latex] and [latex]5[/latex].
- All real numbers less than or equal to [latex]-1[/latex] or greater than or equal to [latex]1[/latex].
- All real numbers less than [latex]-2[/latex] or greater than or equal to [latex]3[/latex].