Comparing Methods for Volume Calculation
We have studied several methods for finding the volume of a solid of revolution, but how do we know which method to use? It often comes down to a choice of which integral is easiest to evaluate.
The figure below describes the different approaches for solids of revolution around the [latex]x\text{-axis}.[/latex] It’s up to you to develop the analogous table for solids of revolution around the [latex]y\text{-axis}.[/latex]
![This figure is a table comparing the different methods for finding volumes of solids of revolution. The columns in the table are labeled “comparison”, “disk method”, “washer method”, and “shell method”. The rows are labeled “volume formula”, “solid”, “interval to partition”, “rectangles”, “typical region”, and “rectangle”. In the disk method column, the formula is given as the definite integral from a to b of pi times [f(x)]^2. The solid has no cavity in the center, the partition is [a,b], rectangles are vertical, and the typical region is a shaded region above the x-axis and below the curve of f(x). In the washer method column, the formula is given as the definite integral from a to b of pi times [f(x)]^2-[g(x)]^2. The solid has a cavity in the center, the partition is [a,b], rectangles are vertical, and the typical region is a shaded region above the curve of g(x) and below the curve of f(x). In the shell method column, the formula is given as the definite integral from c to d of 2pi times yg(y). The solid is with or without a cavity in the center, the partition is [c,d] rectangles are horizontal, and the typical region is a shaded region above the x-axis and below the curve of g(y).](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/2332/2018/01/11213029/CNX_Calc_Figure_06_03_009.jpg)
Let’s take a look at a couple of additional problems and decide on the best approach to take for solving them.
The tips below can help you decide the best method:
| Axis of Revolution | Method | Variable | Description |
|---|---|---|---|
| [latex]x[/latex]-axis | Disk/washer | [latex]dx[/latex] | Use when revolving around the [latex]x[/latex]-axis and integrating with respect to [latex]x[/latex]. The rectangles are perpendicular to the [latex]x[/latex]-axis. |
| Shell | [latex]dy[/latex] | Use when revolving around the [latex]x[/latex]-axis and integrating with respect to [latex]y[/latex]. The rectangles are parallel to the [latex]x[/latex]-axis. | |
| [latex]y[/latex]-axis | Disk/washer | [latex]dy[/latex] | Use when revolving around the [latex]y[/latex]-axis and integrating with respect to [latex]y[/latex]. The rectangles are perpendicular to the [latex]y[/latex]-axis. |
| Shell | [latex]dx[/latex] | Use when revolving around the [latex]y[/latex]-axis and integrating with respect to [latex]x[/latex]. The rectangles are parallel to the [latex]y[/latex]-axis. |
Most times, functions are presented in terms of [latex]x[/latex]. If possible, keeping things in terms of [latex]x[/latex] is beneficial.
Generally speaking, for an [latex]x[/latex]-axis revolution, a disk/washer method will allow us to avoid rewriting the equation in terms of [latex]y[/latex]. For a [latex]y[/latex]-axis revolution, the shell method will allow us the same advantage.
Using this information, try to draw your rectangles in terms of [latex]dx[/latex], if possible. If this requires you to separate the area, try the [latex]dy[/latex] method!
For each of the following problems, select the best method to find the volume of a solid of revolution generated by revolving the given region around the [latex]x\text{-axis},[/latex] and set up the integral to find the volume (do not evaluate the integral).
- The region bounded by the graphs of [latex]y=x,[/latex] [latex]y=2-x,[/latex] and the [latex]x\text{-axis}.[/latex]
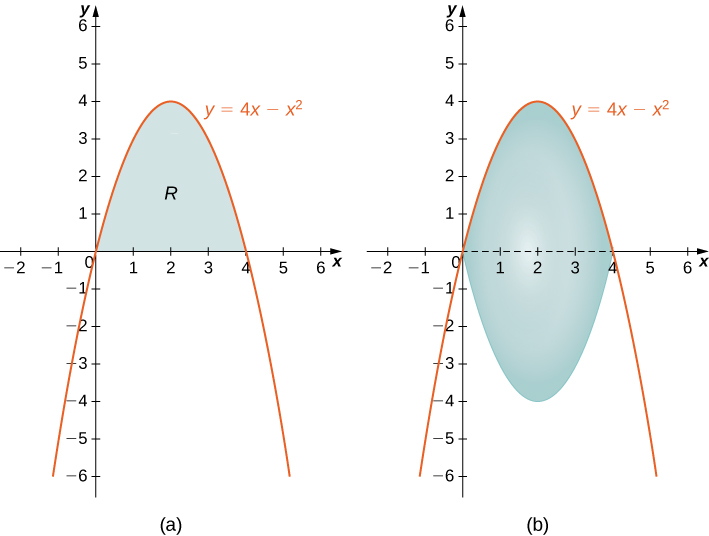
- The region bounded by the graphs of [latex]y=4x-{x}^{2}[/latex] and the [latex]x\text{-axis}.[/latex]
Select the best method to find the volume of a solid of revolution generated by revolving the given region around the [latex]x\text{-axis},[/latex] and set up the integral to find the volume (do not evaluate the integral): the region bounded by the graphs of [latex]y=2-{x}^{2}[/latex] and [latex]y={x}^{2}.[/latex]
Watch the following video to see the worked solution to the two examples above.