Cylindrical Shells Method Cont.

As with the disk method and the washer method, we can use the method of cylindrical shells with solids of revolution, revolved around the [latex]x\text{-axis},[/latex] when we want to integrate with respect to [latex]y.[/latex]

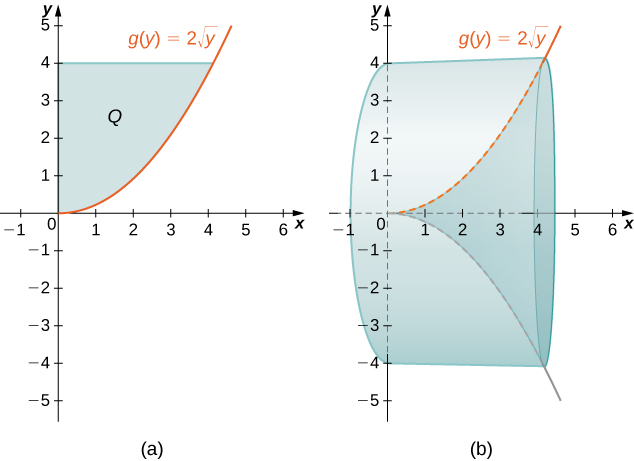
Define [latex]Q[/latex] as the region bounded on the right by the graph of [latex]g(y)=2\sqrt{y}[/latex] and on the left by the [latex]y\text{-axis}[/latex] for [latex]y\in \left[0,4\right].[/latex] Find the volume of the solid of revolution formed by revolving [latex]Q[/latex] around the [latex]x[/latex]-axis.

Show Solution

First, we need to graph the region [latex]Q[/latex] and the associated solid of revolution, as shown in the following figure.

Label the shaded region [latex]Q.[/latex] Then the volume of the solid is given by:

[latex]\begin{array}{cc}\hfill V& ={\displaystyle\int }_{c}^{d}(2\pi yg(y))dy\hfill \\ & ={\displaystyle\int }_{0}^{4}(2\pi y(2\sqrt{y}))dy=4\pi {\displaystyle\int }_{0}^{4}{y}^{3\text{/}2}dy\hfill \\ & ={4\pi \left[\frac{2{y}^{5\text{/}2}}{5}\right]|}_{0}^{4}=\frac{256\pi }{5}{\text{units}}^{3}\text{.}\hfill \end{array}[/latex]

For the next example, we look at a solid of revolution for which the graph of a function is revolved around a line other than one of the two coordinate axes. To set this up, we need to revisit the development of the method of cylindrical shells.

Recall that we found the volume of one of the shells to be given by:

This was based on a shell with an outer radius of [latex]{x}_{i}[/latex] and an inner radius of [latex]{x}_{i-1}.[/latex] If, however, we rotate the region around a line other than the [latex]y\text{-axis},[/latex] we have a different outer and inner radius.

Suppose, for example, that we rotate the region around the line [latex]x=\text{−}k,[/latex] where [latex]k[/latex] is some positive constant. Then, the outer radius of the shell is [latex]{x}_{i}+k[/latex] and the inner radius of the shell is [latex]{x}_{i-1}+k.[/latex]

Substituting these terms into the expression for volume, we see that when a plane region is rotated around the line [latex]x=\text{−}k,[/latex] the volume of a shell is given by:

As before, we notice that [latex]\frac{{x}_{i}+{x}_{i-1}}{2}[/latex] is the midpoint of the interval [latex]\left[{x}_{i-1},{x}_{i}\right][/latex] and can be approximated by [latex]{x}_{i}^{*}.[/latex] Then, the approximate volume of the shell is:

The remainder of the development proceeds as before, and we see that:

We could also rotate the region around other horizontal or vertical lines, such as a vertical line in the right half plane. In each case, the volume formula must be adjusted accordingly. Specifically, the [latex]x\text{-term}[/latex] in the integral must be replaced with an expression representing the radius of a shell. To see how this works, consider the following example.

Define [latex]R[/latex] as the region bounded above by the graph of [latex]f(x)=x[/latex] and below by the [latex]x\text{-axis}[/latex] over the interval [latex]\left[1,2\right].[/latex] Find the volume of the solid of revolution formed by revolving [latex]R[/latex] around the line [latex]x=-1.[/latex]

Show Solution

First, graph the region [latex]R[/latex] and the associated solid of revolution, as shown in the following figure.

Note that the radius of a shell is given by [latex]x+1.[/latex] Then the volume of the solid is given by:

[latex]\begin{array}{cc}\hfill V& ={\displaystyle\int }_{1}^{2}(2\pi (x+1)f(x))dx\hfill \\ & ={\displaystyle\int }_{1}^{2}(2\pi (x+1)x)dx=2\pi {\displaystyle\int }_{1}^{2}({x}^{2}+x)dx\hfill \\ & ={2\pi \left[\frac{{x}^{3}}{3}+\frac{{x}^{2}}{2}\right]|}_{1}^{2}=\frac{23\pi }{3}{\text{units}}^{3}\text{.}\hfill \end{array}[/latex]

For our final example, let’s look at the volume of a solid of revolution for which the region of revolution is bounded by the graphs of two functions.

Define [latex]R[/latex] as the region bounded above by the graph of the function [latex]f(x)=\sqrt{x}[/latex] and below by the graph of the function [latex]g(x)=\frac{1}{x}[/latex] over the interval [latex]\left[1,4\right].[/latex] Find the volume of the solid of revolution generated by revolving [latex]R[/latex] around the [latex]y\text{-axis}.[/latex]

Show Solution

First, graph the region [latex]R[/latex] and the associated solid of revolution, as shown in the following figure.

Note that the axis of revolution is the [latex]y\text{-axis},[/latex] so the radius of a shell is given simply by [latex]x.[/latex] We don’t need to make any adjustments to the [latex]x[/latex]-term of our integrand. The height of a shell, though, is given by [latex]f(x)-g(x),[/latex] so in this case we need to adjust the [latex]f(x)[/latex] term of the integrand.

Then the volume of the solid is given by:

[latex]\begin{array}{cc}\hfill V& ={\displaystyle\int }_{1}^{4}(2\pi x(f(x)-g(x)))dx\hfill \\ & ={\displaystyle\int }_{1}^{4}(2\pi x(\sqrt{x}-\frac{1}{x}))dx=2\pi {\displaystyle\int }_{1}^{4}({x}^{3\text{/}2}-1)dx\hfill \\ & ={2\pi \left[\frac{2{x}^{5\text{/}2}}{5}-x\right]|}_{1}^{4}=\frac{94\pi }{5}{\text{units}}^{3}.\hfill \end{array}[/latex]