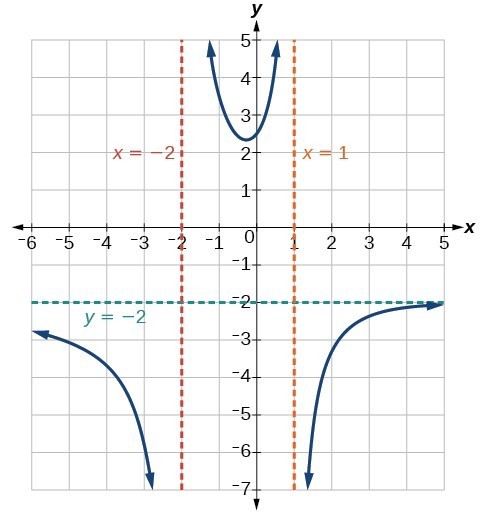
- Find the vertical and horizontal asymptotes of a function
Vertical Asymptote
It’s important to recognize characteristics of a function’s graph that signal specific behaviors. Vertical asymptotes are one such feature, indicating where a function’s output heads towards infinity or negative infinity as the input nears certain values.
vertical asymptote
Vertical asymptotes occur in the graph of a function where the function approaches infinity or negative infinity as the input approaches a certain value. They represent values of [latex]x[/latex] at which the function is undefined and the graph of the function cannot cross. These asymptotes are typically found in rational functions where the denominator is zero.
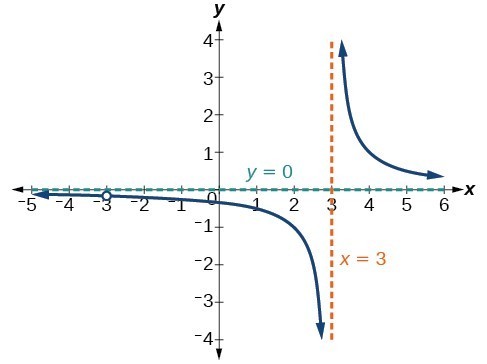
The graph of [latex]f\left(x\right)=\dfrac{x+3}{{x}^{2}-9}[/latex] has a vertical asymptote at [latex]x=3[/latex].
In rational functions, vertical asymptotes serve as crucial indicators of the points at which the function’s value tends toward infinity. These asymptotes can be found by examining the factors of the denominator that do not cancel with corresponding factors in the numerator. Specifically, the values that make the denominator zero—unless they also make the numerator zero—determine the locations of these asymptotes.
How To: Given a Rational Function, Identify it’s Vertical Asymptotes.
- Factor: Break down both the numerator and denominator into their prime factors.
- Simplify: Reduce the rational function by canceling out common factors between the numerator and the denominator.
- Determine Asymptotes: The zeros of the simplified denominator are the [latex]x[/latex]-values for vertical asymptotes, provided they do not also zero the numerator.
To break down an expression into prime factors, repeatedly divide by the smallest prime number that will go into the number evenly, until you reach a quotient of one. For algebraic expressions, apply factoring techniques such as finding common factors, difference of squares, or using the quadratic formula to express the expression as a product of its irreducible factors.
Find the vertical asymptotes of the graph of [latex]k\left(x\right)=\dfrac{5+2{x}^{2}}{2-x-{x}^{2}}[/latex].
Horizontal Asymptote
While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the function that is the ratio of the leading terms.
The leading coefficient and degree of a polynomial function is useful when predicting its end behavior.
If the leading term is positive or negative, and has even or odd degree, it will tell us the toolkit function’s graph behavior it will mimic: [latex]f(x)=x^2, \quad f(x)=-x^2,\quad f(x)=x^3,\quad[/latex] or [latex]\quad f(x)=-x^3[/latex].
The same idea applies to the ratio of leading terms of a rational function.
There are three distinct outcomes when checking for horizontal asymptotes:
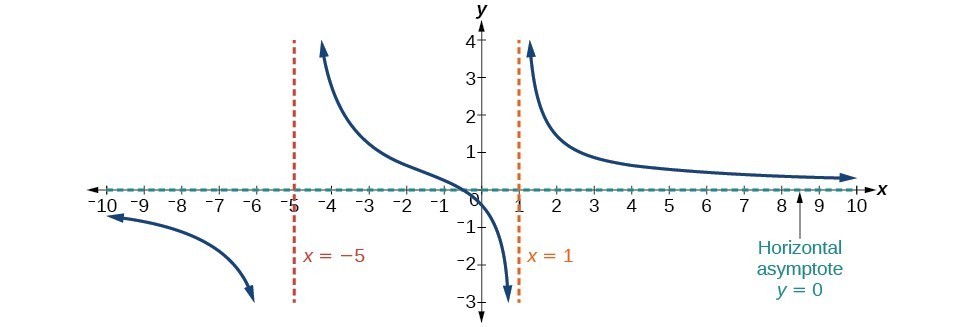
Case 1: If the degree of the denominator is greater than the degree of the numerator, there is a horizontal asymptote at [latex]y=0[/latex].
Consider the following function:
[latex]f\left(x\right)=\dfrac{4x+2}{{x}^{2}+4x - 5}[/latex]
In this case the end behavior is [latex]f\left(x\right)\approx \frac{4x}{{x}^{2}}=\frac{4}{x}[/latex].
This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function [latex]g\left(x\right)=\frac{4}{x}[/latex], and the outputs will approach zero, resulting in a horizontal asymptote at [latex]y=0[/latex]. Note that this graph crosses the horizontal asymptote.
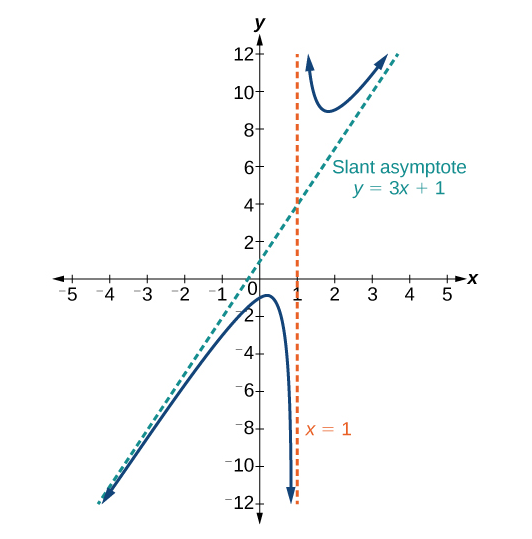
Case 2: If the degree of the denominator is less than the degree of the numerator by one, we get a slant asymptote.
Consider the following function:
[latex]f\left(x\right)=\dfrac{3{x}^{2}-2x+1}{x - 1}[/latex]
In this case the end behavior is [latex]f\left(x\right)\approx \frac{3{x}^{2}}{x}=3x[/latex].
This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function [latex]g\left(x\right)=3x[/latex]. As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote.
However, the graph of [latex]g\left(x\right)=3x[/latex] looks like a diagonal line, and since [latex]f[/latex] will behave similarly to [latex]g[/latex], it will approach a line close to [latex]y=3x[/latex]. This line is a slant asymptote.
To find the equation of the slant asymptote, divide [latex]\dfrac{3{x}^{2}-2x+1}{x - 1}[/latex]. The quotient is [latex]3x+1[/latex] and the remainder is [latex]2[/latex]. The slant asymptote is the graph of the line [latex]g(x)=3x+1[/latex].
Case 3: If the degree of the denominator is equal to the degree of the numerator, there is a horizontal asymptote at [latex]y=\frac{{a}_{n}}{{b}_{n}}[/latex], where [latex]{a}_{n}[/latex] and [latex]{b}_{n}[/latex] are the leading coefficients of [latex]p\left(x\right)[/latex] and [latex]q\left(x\right)[/latex] for [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0[/latex].
Consider the following function:
[latex]f\left(x\right)=\dfrac{3{x}^{2}+2}{{x}^{2}+4x - 5}[/latex]
In this case the end behavior is [latex]f\left(x\right)\approx \frac{3{x}^{2}}{{x}^{2}}=3[/latex].
This tells us that as the inputs grow large, this function will behave like the function [latex]g\left(x\right)=3[/latex], which is a horizontal line. As [latex]x\to \pm \infty ,f\left(x\right)\to 3[/latex], resulting in a horizontal asymptote at [latex]y=3[/latex]. Note that this graph crosses the horizontal asymptote.
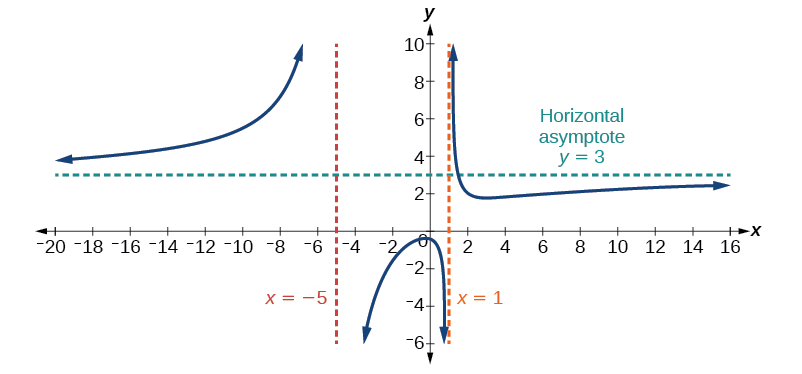
Notice that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.
It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction.
For instance, if we had the function
[latex]f\left(x\right)=\dfrac{3{x}^{5}-{x}^{2}}{x+3}[/latex]
with end behavior
[latex]f\left(x\right)\approx \dfrac{3{x}^{5}}{x}=3{x}^{4}[/latex],
the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.
As [latex]x\to \pm \infty , f\left(x\right)\to \infty[/latex]
horizontal asymptote
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
- Case 1: Degree of denominator [latex]>[/latex] degree of the numerator: horizontal asymptote at [latex]y=0[/latex]
- Case 2: Degree of denominator [latex]<[/latex] degree of numerator by one: no horizontal asymptote; slant asymptote.
- If the degree of the numerator is greater than the degree of the denominator by more than one, the end behavior of the function’s graph will mimic that of the graph of the reduced ratio of leading terms.
- Case 3: Degree of numerator [latex]=[/latex] degree of denominator: horizontal asymptote at ratio of leading coefficients.
For the functions below, identify the horizontal or slant asymptote.
- [latex]g\left(x\right)=\dfrac{6{x}^{3}-10x}{2{x}^{3}+5{x}^{2}}[/latex]
- [latex]h\left(x\right)=\dfrac{{x}^{2}-4x+1}{x+2}[/latex]
- [latex]k\left(x\right)=\dfrac{{x}^{2}+4x}{{x}^{3}-8}[/latex]
Find the horizontal and vertical asymptotes of the function
[latex]f\left(x\right)=\dfrac{\left(x - 2\right)\left(x+3\right)}{\left(x - 1\right)\left(x+2\right)\left(x - 5\right)}[/latex]