Trigonometric Functions: Learn It 2

The Six Basic Trigonometric Functions

Figure 1 shows a right triangle with a vertical side of length [latex]y[/latex] and a horizontal side has length [latex]x[/latex]. Notice that the triangle is inscribed in a circle of radius [latex]1[/latex]. Such a circle, with a center at the origin and a radius of 1, is known as a unit circle.

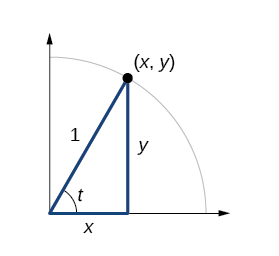
Graph of quarter circle with radius of 1. Inscribed triangle with an angle of t. Point of (x,y) is at intersection of terminal side of angle and edge of circle.
Figure 1

We can define the trigonometric functions in terms an angle [latex]t[/latex] and the lengths of the sides of the triangle. The adjacent side is the side closest to the angle, [latex]x[/latex]. (Adjacent means “next to.”) The opposite side is the side across from the angle, [latex]y[/latex]. The hypotenuse is the side of the triangle opposite the right angle, [latex]1[/latex]. These sides are labeled in the figure below.

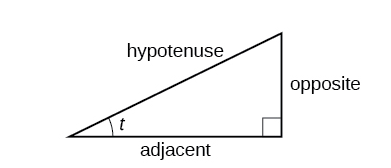
A right triangle with hypotenuse, opposite, and adjacent sides labeled.
Figure 2

Given a right triangle with an acute angle of [latex]t[/latex], the first three trigonometric functions are:

[latex]\begin{array}{ll} \text{Sine} & \sin t = \frac{\text{opposite}}{\text{hypotenuse}} \\ \text{Cosine} & \cos t = \frac{\text{adjacent}}{\text{hypotenuse}} \\ \text{Tangent} & \tan t = \frac{\text{opposite}}{\text{adjacent}} \\ \end{array}[/latex]
A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.”

In addition to sine, cosine, and tangent, there are three more functions. These too are defined in terms of the sides of the triangle.

[latex]\begin{array}{ll} \text{Secant} & \sec t = \frac{\text{hypotenuse}}{\text{adjacent}} \\ \text{Cosecant} & \csc t = \frac{\text{hypotenuse}}{\text{opposite}} \\ \text{Cotangent} & \cot t = \frac{\text{adjacent}}{\text{opposite}} \\ \end{array}[/latex]

Take another look at these definitions. These functions are the reciprocals of the first three functions.

[latex]\begin{array}{ll} \sin t = \frac{1}{\csc t} & \csc t = \frac{1}{\sin t} \\ \cos t = \frac{1}{\sec t} & \sec t = \frac{1}{\cos t} \\ \tan t = \frac{1}{\cot t} & \cot t = \frac{1}{\tan t} \\ \end{array}[/latex]

the six basic trigonometric functions

[latex]\begin{array}{ll} \sin t = \frac{\text{opposite}}{\text{hypotenuse}} & \csc t = \frac{\text{hypotenuse}}{\text{opposite}} \\ \cos t = \frac{\text{adjacent}}{\text{hypotenuse}} & \sec t = \frac{\text{hypotenuse}}{\text{adjacent}} \\ \tan t = \frac{\text{opposite}}{\text{adjacent}} & \cot t = \frac{\text{adjacent}}{\text{opposite}} \\ \end{array}[/latex]

 

If [latex]x=0[/latex], then [latex]\sec \theta[/latex] and [latex]\tan \theta[/latex] are undefined. If [latex]y=0[/latex], then [latex]\cot \theta[/latex] and [latex]\csc \theta[/latex] are undefined.

How to: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles.

  1. If needed, draw the right triangle and label the angle provided.
  2. Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
  3. Find the required function:
    • sine as the ratio of the opposite side to the hypotenuse
    • cosine as the ratio of the adjacent side to the hypotenuse
    • tangent as the ratio of the opposite side to the adjacent side
    • secant as the ratio of the hypotenuse to the adjacent side
    • cosecant as the ratio of the hypotenuse to the opposite side
    • cotangent as the ratio of the adjacent side to the opposite side 

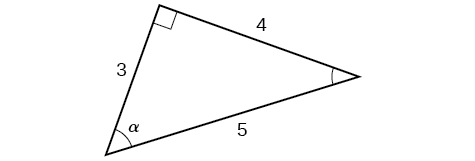
Using the triangle shown in the figure below, evaluate [latex]\sin α[/latex],[latex]\cos α[/latex],[latex]\tan α[/latex],[latex]\sec α[/latex],[latex]\csc α[/latex],and [latex]\cot α[/latex].

Right triangle with sides of 3, 4, and 5. Angle alpha is also labeled which is opposite the side labeled 4.

The real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides. Sine, cosine, and tangent are crucial for calculating an unknown side length in a right triangle.

How to: Use Trigonometric Functions to Find Unknown Side Lengths

  1. Identify the Known Angles and Sides: Determine which sides of the triangle you know (adjacent, opposite, hypotenuse) in relation to the angle you are working with.
  2. Choose the Appropriate Trigonometric Function: Depending on which sides you know and which side you need to find, select the trigonometric function that relates them:
    • Sine (sin) for opposite and hypotenuse.
    • Cosine (cos) for adjacent and hypotenuse.
    • Tangent (tan) for opposite and adjacent.
  3. Set Up the Equation: Use the trigonometric function to set up an equation that relates the known sides and the unknown side.
  4. Solve for the Unknown: Rearrange the equation to solve for the unknown side length. 
Find the unknown sides of the triangle in Figure 11.

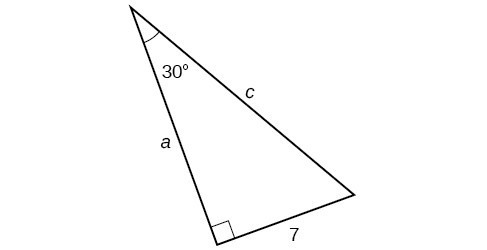
A right triangle with sides a, c, and 7. Angle of 30 degrees is also labeled.
Figure 11

A wooden ramp is to be built with one end on the ground and the other end at the top of a short staircase. If the top of the staircase is [latex]4[/latex] ft from the ground and the angle between the ground and the ramp is to be [latex]10^{\circ}[/latex], how long does the ramp need to be?