- Convert angle measures between degrees and radians
- Interpret and apply basic trigonometric definitions and identities
- Analyze trigonometric functions by identifying graphs and periods, and describing shifts in sine or cosine graphs.
Degrees versus Radians
The Main Idea
- Degrees:
- One degree is [latex]\frac{1}{360}[/latex] of a full circular rotation
- Full circle = [latex]360°[/latex]
- Symbol: [latex]°[/latex] (e.g., [latex]45°[/latex])
- Radians:
- Based on the radius of a circle
- One radian is the angle subtended by an arc length equal to the radius
- Full circle = [latex]2π[/latex] radians
- Symbol: rad (e.g., [latex]\frac{π}{2}[/latex] rad)
- Conversion:
- [latex]π[/latex] radians [latex]= 180°[/latex]
- [latex]1[/latex] radian [latex]≈ 57.3°[/latex]
- Conversion formulas:
- Degrees to Radians: [latex]\text{Angle in Degrees} = \text{Angle in Radians }\times\frac{180}{π}[/latex]
- Radians to Degrees: [latex]\text{Angle in Radians} = \text{Angle in Degrees }\times\frac{π}{180}[/latex]
- Usage:
- Degrees: common in everyday situations, navigation, construction
- Radians: preferred in advanced mathematics, physics, engineering
- Express [latex]210°[/latex] using radians.
- Express [latex]\dfrac{11\pi}{6}[/latex] rad using degrees.
The Six Basic Trigonometric Functions
The Main Idea
- The Six Functions:
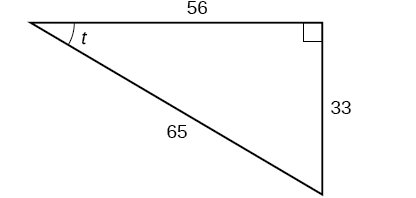
- Sine ([latex]\sin[/latex]): [latex]\frac{\text{opposite}}{\text{hypotenuse}}[/latex]
- Cosine ([latex]\cos[/latex]): [latex]\frac{\text{adjacent}}{\text{hypotenuse}}[/latex]
- Tangent ([latex]\tan[/latex]): [latex]\frac{\text{opposite}}{\text{adjacent}}[/latex]
- Cosecant ([latex]\csc[/latex]): [latex]\frac{\text{hypotenuse}}{\text{opposite}}[/latex] (reciprocal of sine)
- Secant ([latex]\sec[/latex]): [latex]\frac{\text{hypotenuse}}{\text{adjacent}}[/latex] (reciprocal of cosine)
- Cotangent ([latex]\cot[/latex]): [latex]\frac{\text{adjacent}}{\text{opposite}}[/latex] (reciprocal of tangent)
- Mnemonic Device:
- SOH-CAH-TOA for sine, cosine, and tangent
- Reciprocal Relationships:
- [latex]\sin{\theta} = \frac{1}{\csc{\theta}}[/latex]
- [latex]\cos{\theta} = \frac{1}{\sec{\theta}}[/latex]
- [latex]\tan{\theta} = \frac{1}{\cot{\theta}}[/latex]
- Applications:
- Finding unknown side lengths in right triangles
- Solving real-world problems involving angles and distances
A house painter wants to lean a [latex]20[/latex]-ft ladder against a house. If the angle between the base of the ladder and the ground is to be [latex]60^{\circ}[/latex], how far from the house should she place the base of the ladder?
Trigonometric Identities
The Main Idea
- Trigonometric identities are equations involving trigonometric functions that are true for all values where they are defined.
- Types of Identities:
- Reciprocal Identities (e.g., [latex]\csc \theta =\large \frac{1}{\sin \theta}[/latex])
- Pythagorean Identities (e.g., [latex]\sin^2 \theta +\cos^2 \theta =1[/latex])
- Addition and Subtraction Formulas
- Double-Angle Formulas
- Importance:
- Crucial for solving trigonometric equations
- Used in proving other mathematical statements
- Frequently applied in calculus and higher mathematics
- Verification Methods:
- Manipulate one side of the equation to match the other
- Use known identities to make substitutions
- Convert all terms to sines and cosines if needed
Prove the trigonometric identity [latex]1+\cot^2 \theta =\csc^2 \theta[/latex].
Simplify the expression by rewriting and using identities:
[latex]\csc^2{\theta}-\cot^2{\theta}[/latex]
Graphs and Periods of the Trigonometric Functions
The Main Idea
- Periodicity:
- Trigonometric functions repeat their values at regular intervals
- Sine, cosine, secant, cosecant: period of [latex]2π[/latex]
- Tangent, cotangent: period of [latex]π[/latex]
- Basic Graphs:
- Sine and cosine: smooth wave patterns
- Tangent and cotangent: repeating vertical asymptotes
- Secant and cosecant: repeating reciprocal patterns of cosine and sine
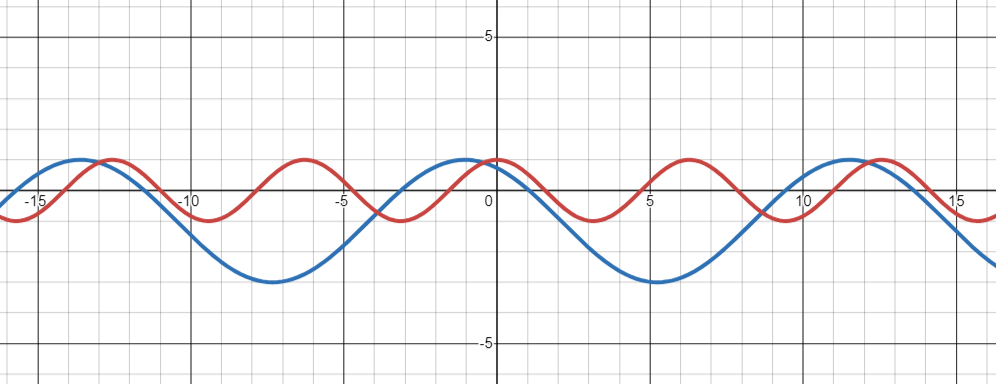
- Transformations: General form: [latex]f(x) = A \sin{(B(x - α))} + C[/latex](similar for cosine)
- [latex]A[/latex]: Amplitude (vertical stretch/compression)
- [latex]B[/latex]: Frequency (horizontal stretch/compression, affects period)
- [latex]α[/latex]: Phase shift (horizontal shift)
- [latex]C[/latex]: Vertical shift
- Effects of Transformations:
- Amplitude: [latex]|A|[/latex] is the height from midline to peak/trough
- Period: [latex]d\frac{2 \pi}{|B|}[/latex] for sine and cosine
- Phase Shift: Right by [latex]α[/latex] if positive, left if negative
- Vertical Shift: Up by [latex]C[/latex] if positive, down if negative
Describe and sketch the graph of [latex]f(x) = 2 \cos{(\frac{1}{2}(x + \frac{π}{3}))} - 1[/latex]
[latex]\pi[/latex] radians is equal to [latex]180^{\circ}[/latex].