The Precise Definition of a Limit: Learn It 3

Lumen Learning

The Precise Definition of a Limit: Learn It 3

One-Sided and Infinite Limits

One-Sided Limits

After gaining an intuitive understanding of limits and moving to a more rigorous definition, we now revisit one-sided limits. We modify the epsilon-delta definition of a limit to give formal definitions for limits from the right and left at a point. These definitions only require slight modifications from the standard limit definition. In the definition of the limit from the right, the inequality $0 < x-a < \delta$ replaces $0 < |x-a| < \delta$ , which ensures that we only consider values of $x$ that are greater than (to the right of) $a$ . Similarly, in the definition of the limit from the left, the inequality $-\delta < x-a < 0$ replaces $0 < |x-a| < \delta$ , which ensures that we only consider values of $x$ that are less than (to the left of) $a$ .

one-sided limits definitions

Limit from the Right: Let $f(x)$ be defined over an open interval of the form $(a,b)$ where $a < b$ . Then,

lim_{x \to a^{+}} f (x) = L

$\underset{x\to a^+}{\lim}f(x)=L$

if for every $\varepsilon >0$ , there exists a $\delta >0$ such that if $0 < x-a < \delta$ , then $|f(x)-L|<\varepsilon$ .

Limit from the Left: Let $f(x)$ be defined over an open interval of the form $(a,b)$ where $a < b$ . Then,

lim_{x \to b^{-}} f (x) = L

$\underset{x\to b^-}{\lim}f(x)=L$

if for every $\varepsilon >0$ , there exists a $\delta >0$ such that if $0 < b-x < \delta$ , then $|f(x)-L|<\varepsilon$ .

Prove that $\underset{x\to 4^+}{\lim}\sqrt{x-4}=0$ .

Let $\varepsilon >0.$

Choose $\delta =\varepsilon^2$ . Since we ultimately want $|\sqrt{x-4}-0|<\varepsilon$ , we manipulate this inequality to get $\sqrt{x-4}<\varepsilon$ or, equivalently, $0 < x-4 < \varepsilon^2$ , making $\delta =\varepsilon^2$ a clear choice.

Assume $0 < x-4 < \delta$ . Thus, $0 < x-4 < \varepsilon^2$ . Hence, $0<\sqrt{x-4}<\varepsilon$ . Finally, $|\sqrt{x-4}-0|<\varepsilon$ .

Therefore, $\underset{x\to 4^+}{\lim}\sqrt{x-4}=0$ .

Watch the following video to see the worked solution to this example.

Closed Captioning and Transcript Information for Video

For closed captioning, open the video on its original page by clicking the Youtube logo in the lower right-hand corner of the video display. In YouTube, the video will begin at the same starting point as this clip, but will continue playing until the very end.

You can view the transcript for this segmented clip of “2.5 Precise Definition of a Limit” here (opens in new window).

Infinite Limits

To understand infinite limits, we look at how functions behave as $x$ approaches a certain value $a$ . For $\underset{x\to a}{\lim}f(x)=+\infty$ , we want $f(x)$ to get arbitrarily large as $x$ approaches $a$ . Instead of the requirement that $|f(x)-L|<\varepsilon$ for arbitrarily small $\varepsilon$ when $0<|x-a|<\delta$ for small enough $\delta$ , we want $f(x)>M$ for arbitrarily large positive $M$ when $0<|x-a|<\delta$ for small enough $\delta$ . The figure below illustrates this idea by showing the value of $\delta$ for successively larger values of $M$ .

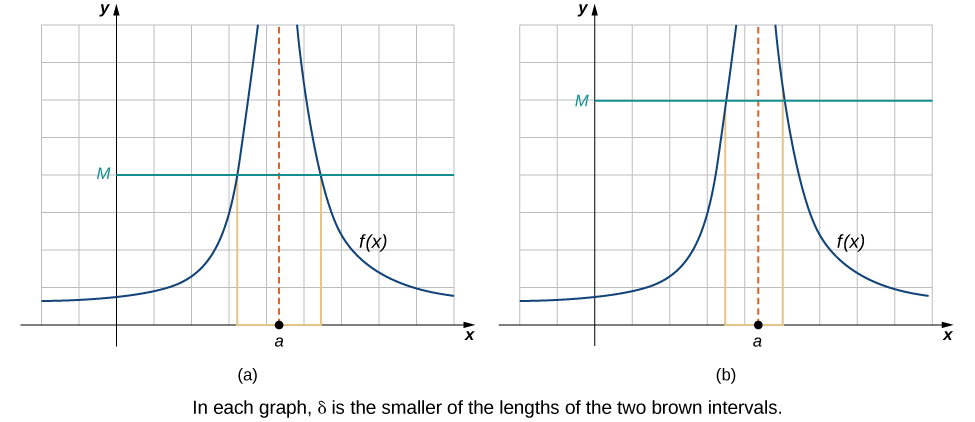
Two graphs side by side. Each graph contains two curves above the x axis separated by an asymptote at x=a. The curves on the left go to infinity as x goes to a and to 0 as x goes to negative infinity. The curves on the right go to infinity as x goes to a and to 0 as x goes to infinity. The first graph has a value M greater than zero marked on the y axis and a horizontal line drawn from there (y=M) to intersect with both curves. Lines are drawn down from the points of intersection to the x axis. Delta is the smaller of the distances between point a and these new spots on the x axis. The same lines are drawn on the second graph, but this M is larger, and the distances from the x axis intersections to point a are smaller. — Figure 6. These graphs plot values of $\delta$ for $M$ to show that $\underset{x\to a}{\lim}f(x)=+\infty$ .

infinite limit definition

Let $f(x)$ be defined for all $x\ne a$ in an open interval containing $a$ . Then, we have an infinite limit

lim_{x \to a} f (x) = + \infty

$\underset{x\to a}{\lim}f(x)=+\infty$

if for every $M>0$ , there exists $\delta >0$ such that if $0<|x-a|<\delta$ , then $f(x)>M$ .

Let $f(x)$ be defined for all $x\ne a$ in an open interval containing $a$ . Then, we have a negative infinite limit

lim_{x \to a} f (x) = - \infty

$\underset{x\to a}{\lim}f(x)=−\infty$

if for every $M>0$ , there exists $\delta >0$ such that if $0<|x-a|<\delta$ , then $f(x)<−M$ .