The Mean Value Theorem: Learn It 1

  • Use Rolle’s theorem and the Mean Value Theorem to show how functions behave between two points
  • Discuss three key implications of the Mean Value Theorem for understanding function behavior

The Mean Value Theorem

The Mean Value Theorem is one of the most important theorems in calculus. We look at some of its implications at the end of this section. First, let’s start with a special case of the Mean Value Theorem, called Rolle’s theorem.

Rolle’s Theorem

Informally, Rolle’s theorem states that if the outputs of a differentiable function [latex]f[/latex] are equal at the endpoints of an interval, then there must be an interior point [latex]c[/latex] where [latex]f^{\prime}(c)=0[/latex]. Figure 1 illustrates this theorem.

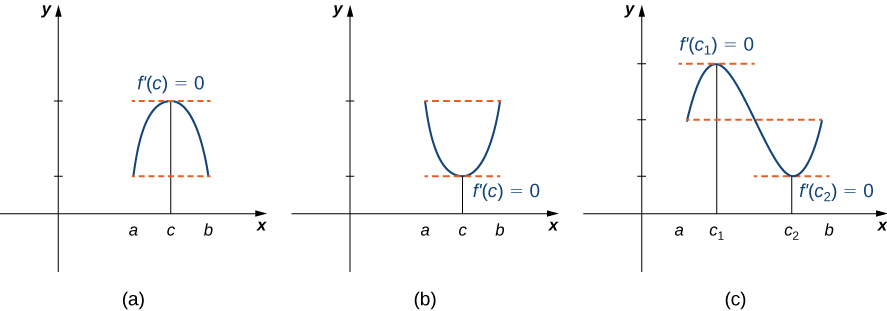
The figure is divided into three parts labeled a, b, and c. Figure a shows the first quadrant with values a, c, and b marked on the x-axis. A downward-facing parabola is drawn such that its values at a and b are the same. The point c is the global maximum, and it is noted that f’(c) = 0. Figure b shows the first quadrant with values a, c, and b marked on the x-axis. An upward-facing parabola is drawn such that its values at a and b are the same. The point c is the global minimum, and it is noted that f’(c) = 0. Figure c shows the first quadrant with points a, c1, c2, and b marked on the x-axis. One period of a sine wave is drawn such that its values at a and b are equal. The point c1 is the global maximum, and it is noted that f’(c1) = 0. The point c2 is the global minimum, and it is noted that f’(c2) = 0.
Figure 1. If a differentiable function f satisfies [latex]f(a)=f(b)[/latex], then its derivative must be zero at some point(s) between [latex]a[/latex] and [latex]b[/latex].

Rolle’s theorem

Let [latex]f[/latex] be a continuous function over the closed interval [latex][a,b][/latex] and differentiable over the open interval [latex](a,b)[/latex] such that [latex]f(a)=f(b)[/latex]. There then exists at least one [latex]c \in (a,b)[/latex] such that [latex]f^{\prime}(c)=0[/latex].

Proof

Let [latex]k=f(a)=f(b)[/latex]. We consider three cases:

  1. [latex]f(x)=k[/latex] for all [latex]x \in (a,b)[/latex].
  2. There exists [latex]x \in (a,b)[/latex] such that [latex]f(x)>k[/latex].
  3. There exists [latex]x \in (a,b)[/latex] such that [latex]f(x)

Case 1: If [latex]f(x)=k[/latex] for all [latex]x \in (a,b)[/latex], then [latex]f^{\prime}(x)=0[/latex] for all [latex]x \in (a,b)[/latex].

Case 2: Since [latex]f[/latex] is a continuous function over the closed, bounded interval [latex][a,b][/latex], by the extreme value theorem, it has an absolute maximum. Also, since there is a point [latex]x \in (a,b)[/latex] such that [latex]f(x)>k[/latex], the absolute maximum is greater than [latex]k[/latex]. Therefore, the absolute maximum does not occur at either endpoint. As a result, the absolute maximum must occur at an interior point [latex]c \in (a,b)[/latex]. Because [latex]f[/latex] has a maximum at an interior point [latex]c[/latex], and [latex]f[/latex] is differentiable at [latex]c[/latex], by Fermat’s theorem, [latex]f^{\prime}(c)=0[/latex].

Case 3: The case when there exists a point [latex]x \in (a,b)[/latex] such that [latex]f(x)

[latex]_\blacksquare[/latex]

An important point about Rolle’s theorem is that the differentiability of the function [latex]f[/latex] is critical. If [latex]f[/latex] is not differentiable, even at a single point, the result may not hold.

For example, the function [latex]f(x)=|x|-1[/latex] is continuous over [latex][-1,1][/latex] and [latex]f(-1)=0=f(1)[/latex], but [latex]f^{\prime}(c) \ne 0[/latex] for any [latex]c \in (-1,1)[/latex] as shown in the following figure.

The function f(x) = |x| − 1 is graphed. It is shown that f(1) = f(−1), but it is noted that there is no c such that f’(c) = 0.
Figure 2. Since [latex]f(x)=|x|-1[/latex] is not differentiable at [latex]x=0[/latex], the conditions of Rolle’s theorem are not satisfied. In fact, the conclusion does not hold here; there is no [latex]c \in (-1,1)[/latex] such that [latex]f^{\prime}(c)=0[/latex].

Let’s now consider functions that satisfy the conditions of Rolle’s theorem and calculate explicitly the points [latex]c[/latex] where [latex]f^{\prime}(c)=0[/latex].

For each of the following functions, verify that the function satisfies the criteria stated in Rolle’s theorem and find all values [latex]c[/latex] in the given interval where [latex]f^{\prime}(c)=0[/latex].

  1. [latex]f(x)=x^2+2x[/latex] over [latex][-2,0][/latex]
  2. [latex]f(x)=x^3-4x[/latex] over [latex][-2,2][/latex]

Verify that the function [latex]f(x)=2x^2-8x+6[/latex] defined over the interval [latex][1,3][/latex] satisfies the conditions of Rolle’s theorem. Find all points [latex]c[/latex] guaranteed by Rolle’s theorem.

Watch the following video to see the worked solution to the two previous examples.