The Limit Laws: Learn It 3

Lumen Learning

The Limit Laws: Learn It 3

The Squeeze Theorem

The techniques we have developed thus far work very well for algebraic functions, but we are still unable to evaluate limits of very basic trigonometric functions.

The next theorem, called the squeeze theorem, proves very useful for establishing basic trigonometric limits.

This theorem allows us to calculate limits by “squeezing” a function, with a limit at a point $a$ that is unknown, between two functions having a common known limit at $a$ .

A graph of three functions over a small interval. All three functions curve. Over this interval, the function g(x) is trapped between the functions h(x), which gives greater y values for the same x values, and f(x), which gives smaller y values for the same x values. The functions all approach the same limit when x=a. — Figure 5. The Squeeze Theorem applies when $f(x)\le g(x)\le h(x)$ and $\underset{x\to a}{\lim}f(x)=\underset{x\to a}{\lim}h(x)$ .

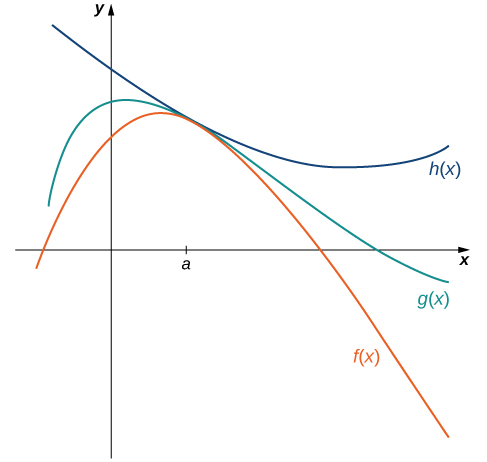
The Squeeze Theorem

Let $f(x), \, g(x)$ , and $h(x)$ be defined for all $x\ne a$ over an open interval containing $a$ . If

g (x) \leq f (x) \leq h (x)

$g(x)\le f(x)\le h(x)$

for all $x\ne a$ in an open interval containing $a$ and

lim_{x \to a} g (x) = L = lim_{x \to a} h (x)

$\underset{x\to a}{\lim}g(x)=L=\underset{x\to a}{\lim}h(x)$

where $L$ is a real number, then $\underset{x\to a}{\lim}f(x)=L$ .

How To: Solve Trigonometric Limits Using the Squeeze Theorem

Confirm the function shows an indeterminate form that the Squeeze Theorem can address.
Find two bounding functions, $g(x)$ and $h(x)$ , that satisfy $g(x)\le f(x)\le h(x)$ .
Ensure $g(x)$ and $h(x)$ approach the same limit at the point of interest.
Use the established bounds to deduce the limit of $f(x)$ . If $g(x)$ and $h(x)$ have a common limit $L$ , then $\underset{x\to a}{\lim}f(x)=L$ .

Apply the Squeeze Theorem to evaluate the limit $\underset{x\to 0}{\lim}\frac{\sin{x^2}}{x}$ .

First start by identify bounding functions. We know that $-1\le \sin{x^2}\le 1$ .

Next, divide these inequalities by $x$ .

$\frac{-1}{x}\le \sin{x^2}\le \frac{1}{x}$

Now, evaluate the limits of the bounding functions as $x$ approaches $0$ .

Both $\frac{-1}{x}$ and $\frac{1}{x}$ approach infinity as $x$ approaches $0$ , but since $\frac{\sin{x^2}}{x}$ is sandwiched between them, we deduce that

$\underset{x\to 0}{\lim}\frac{\sin{x^2}}{x}=0$

due to the squeeze theorem.

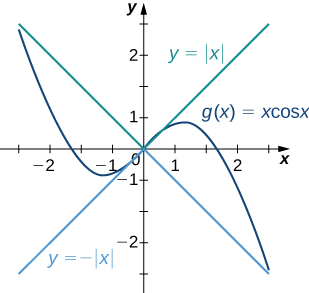
Apply the Squeeze Theorem to evaluate $\underset{x\to 0}{\lim}x \cos x$ .

To evaluate $\underset{x\to 0}{\lim}x \cos x$ using the Squeeze Theorem:

Recognize that $-1\le \cos x\le 1$ for all real numbers.
Multiply this inequality by $x$ to get $-|x|\le x \cos x\le |x|$
As $x$ approaches $0$ , both $−∣x∣$ and $∣x∣$ approach $0$ .
By the Squeeze Theorem, since $x\cos{x}$ is squeezed between two functions that both approach $0$ , $\underset{x\to 0}{\lim}x \cos x=0$ . The graphs of $f(x)=-|x|, \, g(x)=x \cos x$ , and $h(x)=|x|$ are shown in Figure 6.

The graph of three functions: h(x) = x, f(x) = -x, and g(x) = xcos(x). The first, h(x) = x, is a linear function with slope of 1 going through the origin. The second, f(x), is also a linear function with slope of −1; going through the origin. The third, g(x) = xcos(x), curves between the two and goes through the origin. It opens upward for x>0 and downward for x>0. — Figure 6. The graphs of 𝑓(𝑥), 𝑔(𝑥), and ℎ(𝑥) are shown around the point 𝑥=0.